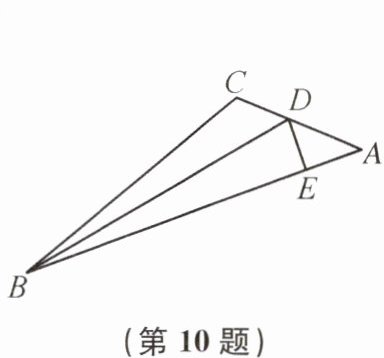
10. (无锡市宜兴市期中)如图,已知$BD是\angle ABC$的平分线,$DE\perp AB于点E$,$AB = 36\ \text{cm}$,$BC = 24\ \text{cm}$,$S_{\triangle ABC} = 144\ \text{cm}^{2}$,则$DE$的长是(
A.$4.8\ \text{cm}$
B.$4.5\ \text{cm}$
C.$4\ \text{cm}$
D.$2.4\ \text{cm}$
A
)
A.$4.8\ \text{cm}$
B.$4.5\ \text{cm}$
C.$4\ \text{cm}$
D.$2.4\ \text{cm}$
答案:
A 提示:过点 D 作 $DF \perp BC$ 交 BC 的延长线于点 F. 因为 BD 是 $\angle ABC$ 的平分线,$DE \perp AB$ 于点 E,所以 $DE = DF$. 因为 $S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle BCD}$,所以 $\frac{1}{2} × 36DE+\frac{1}{2} × 24DF = 144$,即 $18DE + 12DE = 144$,所以 $DE = 4.8\ cm$.
11. (南京市期中)如图,$AD为等边三角形ABC$的高,$E$,$F分别为线段AD$,$AC$上的动点,且$AE = CF$.当$BF + CE$取得最小值时,$\angle AFB = $
$105^{\circ}$
.
答案:
$105^{\circ}$ 提示:在 BC 上方作 $CH \perp BC$,取 $CH = BC$,连接 BH,FH. 因为 $\triangle ABC$ 是等边三角形,$AD \perp BC$,所以 $AC = BC = CH$,$\angle DAC = 30^{\circ}$. 因为 $\angle BCH = 90^{\circ}$,$\angle ACB = 60^{\circ}$,所以 $\angle ACH = 30^{\circ} = \angle DAC$. 又因为 $AE = CF$,所以 $\triangle AEC \cong \triangle CFH$,所以 $CE = HF$,所以 $BF + CE = BF + HF$. 当 F 为 AC 与 BH 的交点时,$BF + CE$ 取得最小值,此时 $\angle FBC = 45^{\circ}$. 因为 $\angle FCB = 60^{\circ}$,所以 $\angle AFB = \angle FBC + \angle FCB = 105^{\circ}$.
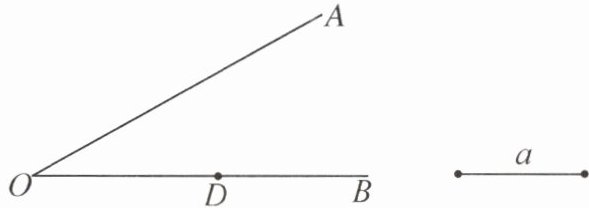
12. (无锡市期中)如图,已知$D为射线OB$上的一点,按下列要求进行作图.
(1)作$\angle AOB的平分线OC$.
(2)在射线$OC上取一点P$,使得$OP = a$.
(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在射线$OA上取一点E$,使得$PE = PD$,这时他发现$\angle OEP与\angle ODP$之间存在一定的数量关系,请写出$\angle OEP与\angle ODP$之间的数量关系,并说明理由.
(1)作$\angle AOB的平分线OC$.
(2)在射线$OC上取一点P$,使得$OP = a$.
(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在射线$OA上取一点E$,使得$PE = PD$,这时他发现$\angle OEP与\angle ODP$之间存在一定的数量关系,请写出$\angle OEP与\angle ODP$之间的数量关系,并说明理由.

答案:
解:(1)如图 1,射线 OC 即为所求.
(2)如图 1,点 P 即为所求.

(3)$\angle OEP = \angle ODP$ 或 $\angle OEP + \angle ODP = 180^{\circ}$. 理由如下:
如图 2,以点 P 为圆心,PD 的长为半径画弧,交 OA 于点 $E_1$,$E_2$,连接 $PE_1$,$PE_2$,PD,过点 P 分别作 $PM \perp OA$ 于点 M,$PN \perp OB$ 于点 N,则 $PM = PN$. 在 $Rt\triangle E_1PM$ 和 $Rt\triangle DPN$ 中,$\begin{cases} PE_1 = PD \\ PM = PN \end{cases}$,所以 $Rt\triangle E_1PM \cong Rt\triangle DPN$,所以 $\angle OE_1P = \angle ODP$. 同理可得 $Rt\triangle E_2PM \cong Rt\triangle DPN$,所以 $\angle PE_2M = \angle ODP$,所以 $\angle OE_2P + \angle ODP = \angle OE_2P + \angle PE_2M = 180^{\circ}$.

解:(1)如图 1,射线 OC 即为所求.
(2)如图 1,点 P 即为所求.

(3)$\angle OEP = \angle ODP$ 或 $\angle OEP + \angle ODP = 180^{\circ}$. 理由如下:
如图 2,以点 P 为圆心,PD 的长为半径画弧,交 OA 于点 $E_1$,$E_2$,连接 $PE_1$,$PE_2$,PD,过点 P 分别作 $PM \perp OA$ 于点 M,$PN \perp OB$ 于点 N,则 $PM = PN$. 在 $Rt\triangle E_1PM$ 和 $Rt\triangle DPN$ 中,$\begin{cases} PE_1 = PD \\ PM = PN \end{cases}$,所以 $Rt\triangle E_1PM \cong Rt\triangle DPN$,所以 $\angle OE_1P = \angle ODP$. 同理可得 $Rt\triangle E_2PM \cong Rt\triangle DPN$,所以 $\angle PE_2M = \angle ODP$,所以 $\angle OE_2P + \angle ODP = \angle OE_2P + \angle PE_2M = 180^{\circ}$.

13. (镇江市句容市期中)新定义:我们把两个面积相等但不全等的三角形叫作“积等三角形”.
(1)【初步尝试】如图1,在$\text{Rt}\triangle ABC$中,$\angle C = 90^{\circ}$,$AB = 10$,$BC = 8$,$P为AC$上一点,当$AP = $
(2)【理解运用】如图2,$\triangle ABD与\triangle ACD$为“积等三角形”,若$AB = 2$,$AC = 5$,且线段$AD$的长为正整数,求$AD$的长.
(3)【综合应用】如图3,在$\text{Rt}\triangle ABC$中,$\angle ACB = 90^{\circ}$,分别以$AC$,$AB为边向外作正方形ACFG和正方形ABDE$,连接$EG$,求证:$\triangle AEG与\triangle ABC$为“积等三角形”.
(1)【初步尝试】如图1,在$\text{Rt}\triangle ABC$中,$\angle C = 90^{\circ}$,$AB = 10$,$BC = 8$,$P为AC$上一点,当$AP = $
3
时,$\triangle ABP与\triangle CBP$为“积等三角形”.(2)【理解运用】如图2,$\triangle ABD与\triangle ACD$为“积等三角形”,若$AB = 2$,$AC = 5$,且线段$AD$的长为正整数,求$AD$的长.
解:延长 AD 至点 E,使 $DE = AD$,连接 CE. 因为 $\triangle ABD$ 与 $\triangle ACD$ 为“积等三角形”,所以 $BD = CD$. 易证 $\triangle ADB \cong \triangle EDC$,$EC = AB = 2$. 因为 $AC = 5$,所以 $5 - 2 < AE < 5 + 2$,所以 $3 < 2AD < 7$,所以 $\frac{3}{2} < AD < \frac{7}{2}$. 因为 AD 为正整数,所以 $AD = 2$ 或 $AD = 3$.
(3)【综合应用】如图3,在$\text{Rt}\triangle ABC$中,$\angle ACB = 90^{\circ}$,分别以$AC$,$AB为边向外作正方形ACFG和正方形ABDE$,连接$EG$,求证:$\triangle AEG与\triangle ABC$为“积等三角形”.
证明:过点 E 作 $EH \perp GA$,交 GA 的延长线于点 H. 因为四边形 ABDE 和四边形 ACFG 均为正方形,所以 $AB = AE$,$AG = AC$,$\angle EAB = \angle GAC = \angle HAC = 90^{\circ}$,所以 $\angle EAH + \angle BAH = 90^{\circ} = \angle BAH + \angle BAC$,所以 $\angle BAC = \angle EAH$. 易证 $\triangle ABC \cong \triangle AEH$,所以 $BC = EH$. 因为 $AG = AC$,所以 $S_{\triangle AEG}=\frac{1}{2}AG \cdot EH=\frac{1}{2}AC \cdot BC = S_{\triangle ABC}$. 又由条件可知 $\triangle AEG$ 与 $\triangle ABC$ 不全等,所以 $\triangle AEG$ 与 $\triangle ABC$ 为“积等三角形”.
答案:
(1)3
(2)解:延长 AD 至点 E,使 $DE = AD$,连接 CE. 因为 $\triangle ABD$ 与 $\triangle ACD$ 为“积等三角形”,所以 $BD = CD$. 易证 $\triangle ADB \cong \triangle EDC$,$EC = AB = 2$. 因为 $AC = 5$,所以 $5 - 2 < AE < 5 + 2$,所以 $3 < 2AD < 7$,所以 $\frac{3}{2} < AD < \frac{7}{2}$. 因为 AD 为正整数,所以 $AD = 2$ 或 $AD = 3$.
(3)证明:过点 E 作 $EH \perp GA$,交 GA 的延长线于点 H. 因为四边形 ABDE 和四边形 ACFG 均为正方形,所以 $AB = AE$,$AG = AC$,$\angle EAB = \angle GAC = \angle HAC = 90^{\circ}$,所以 $\angle EAH + \angle BAH = 90^{\circ} = \angle BAH + \angle BAC$,所以 $\angle BAC = \angle EAH$. 易证 $\triangle ABC \cong \triangle AEH$,所以 $BC = EH$. 因为 $AG = AC$,所以 $S_{\triangle AEG}=\frac{1}{2}AG \cdot EH=\frac{1}{2}AC \cdot BC = S_{\triangle ABC}$. 又由条件可知 $\triangle AEG$ 与 $\triangle ABC$ 不全等,所以 $\triangle AEG$ 与 $\triangle ABC$ 为“积等三角形”.
(2)解:延长 AD 至点 E,使 $DE = AD$,连接 CE. 因为 $\triangle ABD$ 与 $\triangle ACD$ 为“积等三角形”,所以 $BD = CD$. 易证 $\triangle ADB \cong \triangle EDC$,$EC = AB = 2$. 因为 $AC = 5$,所以 $5 - 2 < AE < 5 + 2$,所以 $3 < 2AD < 7$,所以 $\frac{3}{2} < AD < \frac{7}{2}$. 因为 AD 为正整数,所以 $AD = 2$ 或 $AD = 3$.
(3)证明:过点 E 作 $EH \perp GA$,交 GA 的延长线于点 H. 因为四边形 ABDE 和四边形 ACFG 均为正方形,所以 $AB = AE$,$AG = AC$,$\angle EAB = \angle GAC = \angle HAC = 90^{\circ}$,所以 $\angle EAH + \angle BAH = 90^{\circ} = \angle BAH + \angle BAC$,所以 $\angle BAC = \angle EAH$. 易证 $\triangle ABC \cong \triangle AEH$,所以 $BC = EH$. 因为 $AG = AC$,所以 $S_{\triangle AEG}=\frac{1}{2}AG \cdot EH=\frac{1}{2}AC \cdot BC = S_{\triangle ABC}$. 又由条件可知 $\triangle AEG$ 与 $\triangle ABC$ 不全等,所以 $\triangle AEG$ 与 $\triangle ABC$ 为“积等三角形”.
查看更多完整答案,请扫码查看


