例3 (徐州市期中)数轴上点A对应的数是-1,点C对应的数是-4,BC⊥AC,垂足为C,且BC= 1,以点A为圆心,AB的长为半径画弧,交数轴于点D,则点D表示的数为
$-1±\sqrt{10}$
.
答案:
$-1±\sqrt{10}$
例4 (常州市期末)如图,在Rt△ABC中,∠BAC= 90°,分别以△ABC的三条边为直角边作三个等腰直角三角形△ABD,△ACE,△BCF.若图中阴影部分的面积$S_1= 6.5,S_2= 3.5,S_3= 5.5,$则S_4= ______.
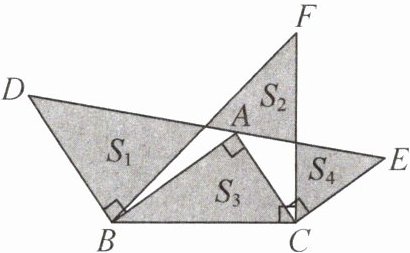
分析 设DE分别交BF,CF于点G,H.因为△ABD,△ACE,△BCF均是等腰直角三角形,所以AB= BD,AC= CE,BC= CF.设AB= BD= a,AC= CE= b,BC= CF= c,S△ABG= m,S△ACH= n.因为$a^2+b^2= c^2,$所以\frac{1}{2}$ a^2$\frac{+1}{2}$ b^2= $\frac{1}{2}$ c^2,$所以S△ABD+S△ACE= S△BCF.因为$S△ABD= S_1+m,S△ACE= n+S_4,S△BCF= S_2+S_3+m+n,$所以$S_1+m+n+S_4= S_2+S_3+m+n,$所以$S_4= S_2+S_3-S_1= 3.5+5.5-6.5= 2.5.$
答案 2.5

分析 设DE分别交BF,CF于点G,H.因为△ABD,△ACE,△BCF均是等腰直角三角形,所以AB= BD,AC= CE,BC= CF.设AB= BD= a,AC= CE= b,BC= CF= c,S△ABG= m,S△ACH= n.因为$a^2+b^2= c^2,$所以\frac{1}{2}$ a^2$\frac{+1}{2}$ b^2= $\frac{1}{2}$ c^2,$所以S△ABD+S△ACE= S△BCF.因为$S△ABD= S_1+m,S△ACE= n+S_4,S△BCF= S_2+S_3+m+n,$所以$S_1+m+n+S_4= S_2+S_3+m+n,$所以$S_4= S_2+S_3-S_1= 3.5+5.5-6.5= 2.5.$
答案 2.5
答案:
2.5
查看更多完整答案,请扫码查看


