7. (泰州市靖江市期中)现有下列说法:①$-4$是16的平方根;②$\sqrt{16}$的算术平方根是4;③$-\sqrt[3]{-2^3} = 2$;④$a的算术平方根是\sqrt{a}$.其中正确的有 (
A.1个
B.2个
C.3个
D.4个
B
)A.1个
B.2个
C.3个
D.4个
答案:
B
8. (泰州市高港区期末)在实数$\frac{1}{3},\frac{\sqrt{2}}{4},\frac{\pi}{6}$中,分数是
$\dfrac{1}{3}$
.
答案:
$\dfrac{1}{3}$
9. (泰州市姜堰区期末)已知实数$a,b,c$在数轴上的对应点如图所示,则$\sqrt{a^2} - |c - a| + \sqrt{(b - c)^2}$的值为 (
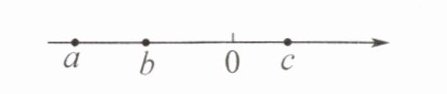
A.$-2a$
B.$-2a - b$
C.$-b$
D.$-2b - a$
C
)
A.$-2a$
B.$-2a - b$
C.$-b$
D.$-2b - a$
答案:
C
10. (泰州市泰兴市期中)已知边长为$m$的正方形的面积为12,下列关于$m$的说法:①$m^2$的值是有理数;②$m的值满足m^2 - 12 = 0$;③$m的值满足不等式组\begin{cases}m - 4 > 0, \\ m - 5 < 0;\end{cases} $④$m$是12的算术平方根.其中正确的有 (
A.1个
B.2个
C.3个
D.4个
C
)A.1个
B.2个
C.3个
D.4个
答案:
C
11. (南京市秦淮区期中)【阅读理解】求$\sqrt{103}$的近似值.
解:设$\sqrt{103} = 10 + x$,其中$0 < x < 1$,则$103 = (10 + x)^2$,即$103 = 100 + 20x + x^2$.因为$0 < x < 1$,所以$0 < x^2 < 1$,所以$103 \approx 100 + 20x$,解得$x \approx 0.15$,即$\sqrt{103}$的近似值为10.15.
【理解应用】利用上面的方法求$\sqrt{95}$的近似值(结果精确到0.01).
解:设$\sqrt{103} = 10 + x$,其中$0 < x < 1$,则$103 = (10 + x)^2$,即$103 = 100 + 20x + x^2$.因为$0 < x < 1$,所以$0 < x^2 < 1$,所以$103 \approx 100 + 20x$,解得$x \approx 0.15$,即$\sqrt{103}$的近似值为10.15.
【理解应用】利用上面的方法求$\sqrt{95}$的近似值(结果精确到0.01).
答案:
解:设$\sqrt{95}=10 - x$,其中$0 < x < 1$,则$95=(10 - x)^{2}$,即$95=100 - 20x+x^{2}$.因为$0 < x < 1$,所以$0 < x^{2}<1$,所以$95\approx100 - 20x$,解得$x\approx0.25$,即$\sqrt{95}$的近似值为9.75.
查看更多完整答案,请扫码查看


