《2025年小题狂做八年级数学上册苏科版提优版》

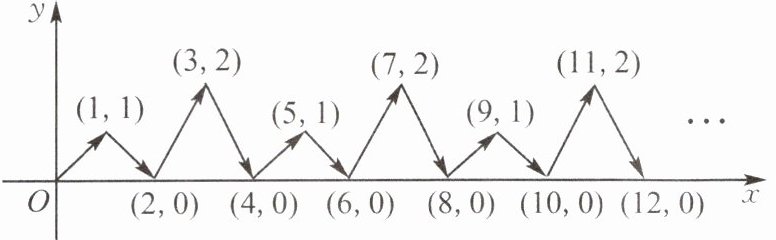
例9 (盐城市大丰区期末)如图,动点P在平面直角坐标系中按图中箭头所示方向运动.第1次从原点运动到点$(1,1)$,第2次接着运动到点$(2,0)$,第3次接着运动到点$(3,2)$,…,按这样的运动规律,经过第2025次运动后,动点P的坐标是____.

分析 从点的坐标可以看出横坐标正好是运动的次数,所以经过第2025次运动后点的横坐标就是2025.纵坐标是1,0,2,0,…,四个一循环,$2025÷4= 506... 1$.因此经过第2025次运动后点的纵坐标是1,故点P的坐标为$(2025,1)$.
答案$(2025,1)$

答案： 【解析】：
首先，我们观察动点P的运动规律。
动点P的横坐标正好等于运动的次数。例如，第1次运动后，横坐标为1；第2次运动后，横坐标为2；以此类推，第2025次运动后，横坐标就是2025。
其次，动点P的纵坐标呈现一个周期性变化的规律，即1，0，2，0四个数一循环。我们可以通过计算2025除以4的余数来确定第2025次运动后动点P的纵坐标。
计算得$2025 ÷ 4 = 506...1$，余数为1，说明第2025次运动后动点P的纵坐标是循环组的第一个数，即1。
综上所述，经过第2025次运动后，动点P的坐标是$(2025,1)$。
【答案】：
$(2025,1)$

例10 (泰州市泰兴市期末)如图,在平面直角坐标系中,分别写出$\triangle ABC$的顶点坐标,并求出$\triangle ABC$的面积.

答案 由题图知,$\triangle ABC的顶点坐标分别是A(2,3)$,$B(-2,-1)$,$C(1,-3)$.所以$S_{\triangle ABC}= 4×6-\frac {1}{2}×4×4-\frac {1}{2}×2×3-\frac {1}{2}×1×6= 10$.

答案： 【解析】：
本题主要考查了在平面直角坐标系中确定点的坐标以及利用割补法求三角形的面积。
确定顶点坐标：通过观察平面直角坐标系中$\triangle ABC$的三个顶点位置，可直接得出顶点$A$、$B$、$C$的坐标。
求三角形面积：采用割补法，先构造一个包含$\triangle ABC$的矩形，然后用矩形的面积减去周围三个直角三角形的面积，从而得到$\triangle ABC$的面积。
【答案】：
解：由题图知，$\triangle ABC$的顶点坐标分别是$A(2,3)$，$B(-2,-1)$，$C(1,-3)$。
$S_{\triangle ABC}=4×6 - \frac{1}{2}×4×4 - \frac{1}{2}×2×3 - \frac{1}{2}×1×6$
$=24 - 8 - 3 - 3$
$=10$