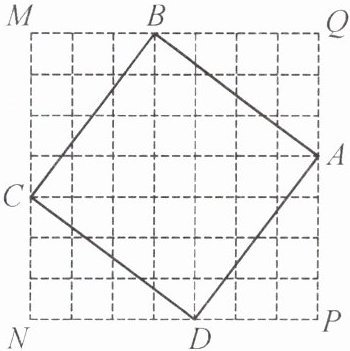
例6 (南通市启东市期末)如图,在正方形网格MNPQ中,每个小方格的边长都相等,正方形ABCD的顶点在正方形MNPQ的四条边的小方格顶点上.设MB= a,BQ= b,利用这个图形中的直角三角形和正方形的面积关系,你能验证已学过的一个数学公式或定理吗?
分析 根据图形之间的面积关系能够验证勾股定理以及完全平方公式.
答案 验证完全平方公式或勾股定理.验证如下:
在△BCM和△ABQ中,{BM= AQ, ∠M= ∠Q, CM= BQ},所以△BCM≌△ABQ.同理,△CDN,△BCM,△ABQ和△DAP全部全等.因为MB= a,BQ= b,S正方形MNPQ= S正方形ABCD+4S△ABQ,所以$(a+b)^2= a^2+b^2+4×1/2 ab,$即$(a+b)^2= a^2+2ab+b^2($完全平方公式).设AB= c.因为S正方形ABCD= S正方形MNPQ-4S△ABQ,所以$c^2= (a+b)^2-4×1/2 ab,$即$c^2= a^2+b^2($勾股定理).
知识链接
完全平方公式:$(a+b)^2= a^2+2ab+b^2.$

分析 根据图形之间的面积关系能够验证勾股定理以及完全平方公式.
答案 验证完全平方公式或勾股定理.验证如下:
在△BCM和△ABQ中,{BM= AQ, ∠M= ∠Q, CM= BQ},所以△BCM≌△ABQ.同理,△CDN,△BCM,△ABQ和△DAP全部全等.因为MB= a,BQ= b,S正方形MNPQ= S正方形ABCD+4S△ABQ,所以$(a+b)^2= a^2+b^2+4×1/2 ab,$即$(a+b)^2= a^2+2ab+b^2($完全平方公式).设AB= c.因为S正方形ABCD= S正方形MNPQ-4S△ABQ,所以$c^2= (a+b)^2-4×1/2 ab,$即$c^2= a^2+b^2($勾股定理).
知识链接
完全平方公式:$(a+b)^2= a^2+2ab+b^2.$
答案:
验证完全平方公式或勾股定理.验证如下:在△BCM和△ABQ中,{BM= AQ, ∠M= ∠Q, CM= BQ},所以△BCM≌△ABQ.同理,△CDN,△BCM,△ABQ和△DAP全部全等.因为MB= a,BQ= b,S正方形MNPQ= S正方形ABCD+4S△ABQ,所以(a+b)²= a²+b²+4×1/2 ab,即(a+b)²= a²+2ab+b²(完全平方公式).设AB= c.因为S正方形ABCD= S正方形MNPQ-4S△ABQ,所以c²= (a+b)²-4×1/2 ab,即c²= a²+b²(勾股定理).
查看更多完整答案,请扫码查看


