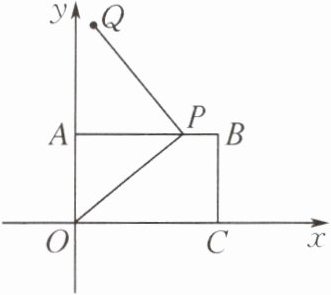
例6 (常州市武进区期中)如图,将长方形OABC放置在平面直角坐标系中,P是折线$A-B-C$上的动点(点P不与点A,C重合),连接OP,将OP绕点P顺时针旋转$90^{\circ }$,点O落到点Q处.已知点B的坐标为$(24,15)$,当$OP= 25$时,点Q的坐标为____.
关键提示
此题考查在平面直角坐标系中平移作图、轴对称变换的知识.解答本题的关键是掌握平移和轴对称的特点,确定各点在平面直角坐标系中的位置.
易错警示
对条件“P是折线$A-B-C$上的动点”要注意分类讨论,即分点P在AB上和在BC上两种情况来逐一画图,分别求解.
关键提示
此题考查在平面直角坐标系中平移作图、轴对称变换的知识.解答本题的关键是掌握平移和轴对称的特点,确定各点在平面直角坐标系中的位置.
易错警示
对条件“P是折线$A-B-C$上的动点”要注意分类讨论,即分点P在AB上和在BC上两种情况来逐一画图,分别求解.

(5,35)或(31,-17)
答案:
解:
情况1:点P在AB上
设P(m,15),A(0,15),B(24,15),则0<m<24。
∵OP=25,
∴由勾股定理得:$m^2 + 15^2 = 25^2$,解得m=20(m=-20舍)。
∴P(20,15)。
过P作PD⊥x轴于D,过Q作QE⊥AB于E,易证△OPD≌△PQE(AAS)。
∴QE=PD=15,PE=OD=20。
∵AB在y=15上,
∴Q的横坐标为20 - 15=5,纵坐标为15 + 20=35。
∴Q(5,35)。
情况2:点P在BC上
设P(24,n),C(24,0),则0<n<15。
∵OP=25,
∴由勾股定理得:$24^2 + n^2 = 25^2$,解得n=7(n=-7舍)。
∴P(24,7)。
过P作PF⊥y轴于F,过Q作QG⊥BC于G,易证△OPF≌△PQG(AAS)。
∴QG=PF=24,PG=OF=7。
∵BC在x=24上,
∴Q的横坐标为24 + 7=31,纵坐标为7 - 24=-17。
∴Q(31,-17)。
综上,点Q的坐标为(5,35)或(31,-17)。
答案:(5,35)或(31,-17)
情况1:点P在AB上
设P(m,15),A(0,15),B(24,15),则0<m<24。
∵OP=25,
∴由勾股定理得:$m^2 + 15^2 = 25^2$,解得m=20(m=-20舍)。
∴P(20,15)。
过P作PD⊥x轴于D,过Q作QE⊥AB于E,易证△OPD≌△PQE(AAS)。
∴QE=PD=15,PE=OD=20。
∵AB在y=15上,
∴Q的横坐标为20 - 15=5,纵坐标为15 + 20=35。
∴Q(5,35)。
情况2:点P在BC上
设P(24,n),C(24,0),则0<n<15。
∵OP=25,
∴由勾股定理得:$24^2 + n^2 = 25^2$,解得n=7(n=-7舍)。
∴P(24,7)。
过P作PF⊥y轴于F,过Q作QG⊥BC于G,易证△OPF≌△PQG(AAS)。
∴QG=PF=24,PG=OF=7。
∵BC在x=24上,
∴Q的横坐标为24 + 7=31,纵坐标为7 - 24=-17。
∴Q(31,-17)。
综上,点Q的坐标为(5,35)或(31,-17)。
答案:(5,35)或(31,-17)
查看更多完整答案,请扫码查看


