《2025年小题狂做八年级数学上册苏科版提优版》

4. (南京市联合体期末)如图,点$A$,$B$,$C$,$D$在同一条直线上,$AC = DB$,$AE = DF$,$AE// DF$.
(1)求证：$\triangle ABE\cong\triangle DCF$；
(2)若$AB = AE$,$\angle A = 46^{\circ}$,求$\angle F$的度数.

答案： （1）证明：因为 $AC = DB$，所以 $AC - BC = DB - BC$，即 $AB = DC$. 因为 $AE // DF$，所以 $\angle A = \angle D$. 又因为 $AE = DF$，所以 $\triangle ABE \cong \triangle DCF(SAS)$.
（2）解：因为 $AB = AE$，$\angle A = 46^{\circ}$，所以 $\angle E = \angle ABE = \frac{1}{2} × (180^{\circ} - \angle A)=67^{\circ}$. 因为 $\triangle ABE \cong \triangle DCF$，所以 $\angle F = \angle E = 67^{\circ}$.

5. (徐州市期末)已知在等腰三角形$ABC$中,$AB = AC$,顶角为$40^{\circ}$.若同一平面内有一点$P$,满足$AP = BC$,且$BP = BA$,则$\angle PBC$的度数为( )

A.$140^{\circ}或60^{\circ}$
B.$110^{\circ}或60^{\circ}$
C.$110^{\circ}或30^{\circ}$
D.$140^{\circ}或30^{\circ}$

答案：
C 提示：如图 1，当点 P 在边 AB 的左侧时，由题意可知，$\angle BAC = 40^{\circ}$，因为 $AB = AC$，$BP = BA$，所以 $\angle ABC = \angle ACB = 70^{\circ}$，$AC = BP$，又因为 $AP = BC$，$AB = BA$，所以 $\triangle ABC \cong \triangle BAP(SSS)$，所以 $\angle PBA = \angle BAC = 40^{\circ}$，所以 $\angle PBC = \angle PBA + \angle ABC = 110^{\circ}$；如图 2，当点 P 在边 AB 的右侧时，同理可得 $\angle PBA = \angle BAC = 40^{\circ}$，所以 $\angle PBC = \angle ABC - \angle PBA = 30^{\circ}$. 综上所述，$\angle PBC$ 的度数为 $110^{\circ}$ 或 $30^{\circ}$.
　　　 　　
易错警示：由于点 P 的位置不确定，需要分类讨论. 若将题中条件“顶角为 $40^{\circ}$”改为“底角为 $40^{\circ}$”，则答案选 A.

6. (南京市秦淮区期中)在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = BC$,分别过点$A$,$B向过点C的直线CD$作垂线,垂足分别为$E$,$F$.若$AE = 3$,$BF = 1$,则$EF$的长为______.

答案：
4 或 2 提示：如图 1、图 2，易证 $\triangle BFC \cong \triangle CEA$，所以 $CF = AE = 3$，$CE = BF = 1$. 所以 $EF = CF + CE = 4$ 或 $EF = CF - CE = 2$.
　　　 　　
易错警示：由于直线 CD 的位置未明确，故需分类讨论，分别画出图形.

7. (连云港市灌南县期中)如图,$\triangle ABC是边长为2$的等边三角形,直线$l经过顶点A$,且与边$BC$平行.在直线$l上有一点P$,当$AP$的长为2 或 4时,$\angle APC = \frac{1}{2}\angle ACB$.

答案： 2 或 4 提示：由题意，得 $AB = AC = BC = 2$，$\angle ACB = \angle BAC = \angle B = 60^{\circ}$. 所以 $\angle APC = \frac{1}{2}\angle ACB = 30^{\circ}$. 当点 P 在点 A 左侧时，因为直线 $l // BC$，所以 $\angle APC = \angle PCB = 30^{\circ}$，因为 $\angle ACB = 60^{\circ}$，所以 $\angle ACP = 30^{\circ}$，所以 $AP = AC = 2$；当点 P 在点 A 右侧时，因为直线 $l // BC$，所以 $\angle PAC = \angle ACB = 60^{\circ}$，又因为 $\angle APC = 30^{\circ}$，所以 $\angle ACP = 90^{\circ}$，所以 $AP = 2AC = 4$. 所以当 AP 的长为 2 或 4 时，$\angle APC = \frac{1}{2}\angle ACB$.

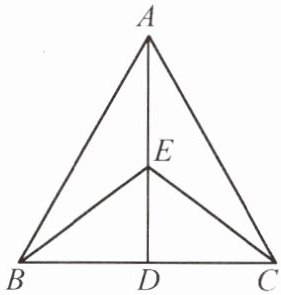
8. (扬州市江都区期中)如图,已知$D是\triangle ABC的边BC$上的一点,$E是线段AD$上的一点,$EB = EC$,$\angle ABE = \angle ACE$.求证：$\angle BAE = \angle CAE$.

答案： 证明：过点 E 分别作 $EF \perp AB$ 于点 F，$EG \perp AC$ 于点 G. 在 $\triangle BEF$ 和 $\triangle CEG$ 中，$\begin{cases} \angle EFB = \angle EGC \\ \angle ABE = \angle ACE \\ EB = EC \end{cases}$，所以 $\triangle BEF \cong \triangle CEG$，所以 $EF = EG$. 在 $Rt\triangle AEF$ 和 $Rt\triangle AEG$ 中，$\begin{cases} AE = AE \\ EF = EG \end{cases}$，所以 $Rt\triangle AEF \cong Rt\triangle AEG$，所以 $\angle BAE = \angle CAE$.
易错警示：虽然条件集中于 $\triangle ABE$ 和 $\triangle ACE$ 中，但利用 $AE = AE$，$\angle ABE = \angle ACE$，$BE = CE$ 无法直接得到 $\triangle ABE \cong \triangle ACE$. 因为三个条件之间的位置关系是“两边及其中一边的对角对应相等”，而不是“两边及其夹角对应相等”，所以不能作为判定两个三角形全等的理论依据.

9. (无锡市江阴市期中)如图,$BD为\triangle ABC$的角平分线,且$BD = BC$,$E为BD$延长线上的一点,$BA = BE$,过点$E作EF\perp AB$,垂足为$F$.现有下列结论：①$\triangle ABD\cong\triangle EBC$；②$\angle BCE + \angle BCD = 180^{\circ}$；③$AD = AE = EC$；④$BA + BC = 2BF$.其中正确的是(D)
A.①②③
B.①③④
C.①②④
D.①②③④

答案： D 提示：因为 BD 为 $\angle ABC$ 的平分线，所以 $\angle ABD = \angle EBC$. 在 $\triangle ABD$ 和 $\triangle EBC$ 中，因为 $BD = BC$，$\angle ABD = \angle EBC$，$BA = BE$，所以 $\triangle ABD \cong \triangle EBC$，故①正确. 因为 $BD = BC$，$BA = BE$，所以 $\angle BCD = \angle BDC$，$\angle BAE = \angle BEA$. 因为 $\triangle ABD \cong \triangle EBC$，所以 $\angle BCE = \angle BDA$，所以 $\angle BCE + \angle BCD = \angle BDA + \angle BDC = 180^{\circ}$，故②正确. 因为 $\angle BCD = \angle BDC = \frac{1}{2} × (180^{\circ} - \angle CBD)$，$\angle BAE = \angle BEA = \frac{1}{2} × (180^{\circ} - \angle ABD)$，$\angle CBD = \angle ABD$，所以 $\angle BCD = \angle BDC = \angle BAE = \angle BEA$. 因为 $\angle BDC = \angle ADE$，所以 $\angle ADE = \angle BEA$，所以 $AD = AE$. 因为 $\triangle ABD \cong \triangle EBC$，所以 $AD = EC$，所以 $AD = AE = EC$，故③正确. 作 $EG \perp BC$，垂足为 G. 易证 $\triangle BEG \cong \triangle BEF$，所以 $BG = BF$，$EG = EF$. 易证 $\triangle AEF \cong \triangle CEG$，所以 $AF = CG$. 所以 $BA + BC = BF + AF + BG - CG = BF + BG = 2BF$，故④正确.