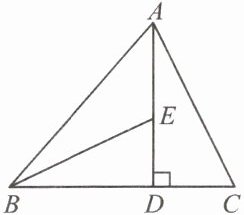
例2 (徐州市期末)如图,$AD是\triangle ABC$的高,$BE平分\angle ABC交AD于点E$.若$\angle C = 70^{\circ}$,$\angle BED = 64^{\circ}$,求$\angle BAC$的度数.

答案:
【解析】:本题可根据三角形高的定义、角平分线的性质以及三角形内角和定理来求解$\angle BAC$的度数。
首先,根据三角形高的定义,因为$AD$是$\triangle ABC$的高,所以$\angle ADC = \angle ADB = 90^{\circ}$。
然后,在$\triangle BDE$中,已知$\angle ADB = 90^{\circ}$,$\angle BED = 64^{\circ}$,根据直角三角形两锐角互余,可求出$\angle DBE$的度数,即$\angle DBE = 90^{\circ} - \angle BED = 90^{\circ} - 64^{\circ} = 26^{\circ}$。
接着,因为$BE$平分$\angle ABC$,根据角平分线的性质,所以$\angle ABC = 2\angle DBE = 2×26^{\circ} = 52^{\circ}$。
最后,在$\triangle ABC$中,已知$\angle C = 70^{\circ}$,$\angle ABC = 52^{\circ}$,根据三角形内角和定理$\angle BAC = 180^{\circ} - \angle C - \angle ABC$,可求出$\angle BAC$的度数。
【答案】:解:因为$AD$是$\triangle ABC$的高,
所以$\angle ADC = \angle ADB = 90^{\circ}$。
又因为$\angle BED = 64^{\circ}$,
所以$\angle DBE = 90^{\circ} - \angle BED = 90^{\circ} - 64^{\circ} = 26^{\circ}$。
因为$BE$平分$\angle ABC$,
所以$\angle ABC = 2\angle DBE = 2×26^{\circ} = 52^{\circ}$。
所以$\angle BAC = 180^{\circ} - \angle C - \angle ABC = 180^{\circ} - 70^{\circ} - 52^{\circ} = 58^{\circ}$。
首先,根据三角形高的定义,因为$AD$是$\triangle ABC$的高,所以$\angle ADC = \angle ADB = 90^{\circ}$。
然后,在$\triangle BDE$中,已知$\angle ADB = 90^{\circ}$,$\angle BED = 64^{\circ}$,根据直角三角形两锐角互余,可求出$\angle DBE$的度数,即$\angle DBE = 90^{\circ} - \angle BED = 90^{\circ} - 64^{\circ} = 26^{\circ}$。
接着,因为$BE$平分$\angle ABC$,根据角平分线的性质,所以$\angle ABC = 2\angle DBE = 2×26^{\circ} = 52^{\circ}$。
最后,在$\triangle ABC$中,已知$\angle C = 70^{\circ}$,$\angle ABC = 52^{\circ}$,根据三角形内角和定理$\angle BAC = 180^{\circ} - \angle C - \angle ABC$,可求出$\angle BAC$的度数。
【答案】:解:因为$AD$是$\triangle ABC$的高,
所以$\angle ADC = \angle ADB = 90^{\circ}$。
又因为$\angle BED = 64^{\circ}$,
所以$\angle DBE = 90^{\circ} - \angle BED = 90^{\circ} - 64^{\circ} = 26^{\circ}$。
因为$BE$平分$\angle ABC$,
所以$\angle ABC = 2\angle DBE = 2×26^{\circ} = 52^{\circ}$。
所以$\angle BAC = 180^{\circ} - \angle C - \angle ABC = 180^{\circ} - 70^{\circ} - 52^{\circ} = 58^{\circ}$。
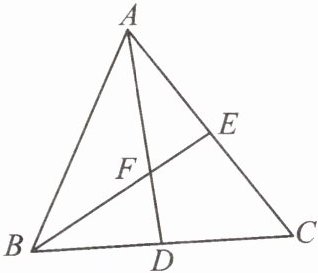
例3 (苏州市工业园区期末)如图,$\triangle ABC的中线AD$,$BE相交于点F$.若$\triangle ABF的面积为1$,则四边形$FDCE$的面积是______.

1
答案:
【解析】:题目考查了三角形的中线性质以及三角形面积的计算。
三角形中线的性质:三角形的中线将三角形分为面积相等的两部分。
因为$AD,BE$是$\triangle ABC$的中线,
所以$D,E$分别是$BC,AC$边上的中点,
所以$S_{\triangle ABD} = \frac{1}{2}S_{\triangle ABC}$,$S_{\triangle BEC} = \frac{1}{2}S_{\triangle ABC}$,
所以$S_{\triangle BEC} = S_{\triangle ABD}$,
所以$S_{四边形FDCE} = S_{\triangle BEC} - S_{\triangle BFD} = S_{\triangle ABD} - S_{\triangle BFD} = S_{\triangle ABF} = 1$。
【答案】:1
三角形中线的性质:三角形的中线将三角形分为面积相等的两部分。
因为$AD,BE$是$\triangle ABC$的中线,
所以$D,E$分别是$BC,AC$边上的中点,
所以$S_{\triangle ABD} = \frac{1}{2}S_{\triangle ABC}$,$S_{\triangle BEC} = \frac{1}{2}S_{\triangle ABC}$,
所以$S_{\triangle BEC} = S_{\triangle ABD}$,
所以$S_{四边形FDCE} = S_{\triangle BEC} - S_{\triangle BFD} = S_{\triangle ABD} - S_{\triangle BFD} = S_{\triangle ABF} = 1$。
【答案】:1
查看更多完整答案,请扫码查看


