第169页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
例题2 如图,从甲地到乙地只允许往南和往东走,不能走重复路线,那么从甲地到乙地一共有多少种不同的路线可走?
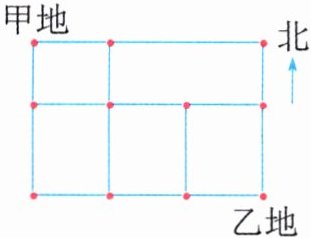
思路导引:方法一:用数字或字母标注路口进行列举。
如图,从甲地到乙地,把必须经过的路口按顺序一一列举出来就可以了。
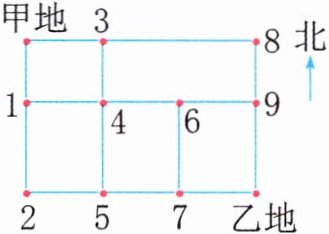
方法二:运用标数法进行列举。
从甲地到乙地往南和往东的两个路口都只有1种走法,分别标上1,其他任何一个交叉点的路线总数都等于通过该点左边和上面的两个邻近交叉点的路线数量的总和。
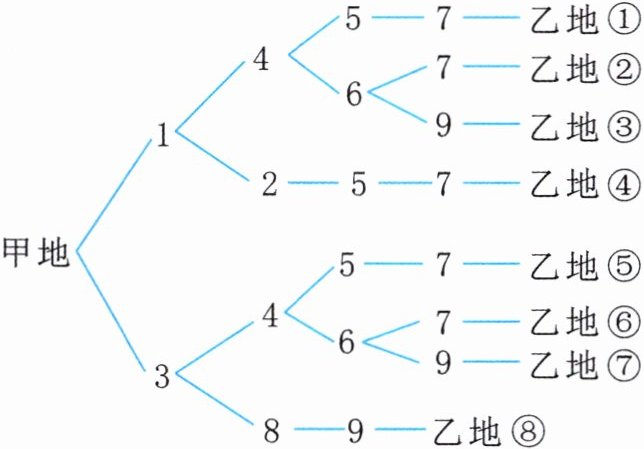
完全解答:方法一:
方法二:

答:从甲地到乙地一共有8种不同的路线可走。
点评苑:遇到此类问题,比较简单的情况可以用方法一解决,比较复杂的情况运用方法二更易于有序找出所有行走路线。

思路导引:方法一:用数字或字母标注路口进行列举。
如图,从甲地到乙地,把必须经过的路口按顺序一一列举出来就可以了。

方法二:运用标数法进行列举。
从甲地到乙地往南和往东的两个路口都只有1种走法,分别标上1,其他任何一个交叉点的路线总数都等于通过该点左边和上面的两个邻近交叉点的路线数量的总和。
完全解答:方法一:

方法二:

答:从甲地到乙地一共有8种不同的路线可走。
点评苑:遇到此类问题,比较简单的情况可以用方法一解决,比较复杂的情况运用方法二更易于有序找出所有行走路线。
答案:
例题1 两个自然数相乘,积是12的乘法算式有多少道?
错误解法:
|一个自然数|12|6|4|
|另一个自然数|1|2|3|
答:积是12的乘法算式有3道。
正确解法:
|一个自然数|12|6|4|3|2|1|
|另一个自然数|1|2|3|4|6|12|
答:积是12的乘法算式有6道。
误点分析:错误解法错在受教材例题中宽要比长短的干扰,把“另一个自然数”也当成要比“一个自然数”小了。其实积是12的两个自然数应该不分大小,是可以交换位置的。
错误解法:
|一个自然数|12|6|4|
|另一个自然数|1|2|3|
答:积是12的乘法算式有3道。
正确解法:
|一个自然数|12|6|4|3|2|1|
|另一个自然数|1|2|3|4|6|12|
答:积是12的乘法算式有6道。
误点分析:错误解法错在受教材例题中宽要比长短的干扰,把“另一个自然数”也当成要比“一个自然数”小了。其实积是12的两个自然数应该不分大小,是可以交换位置的。
答案:
解析:本题考察的是用列举的策略解决实际问题,特别是涉及到自然数相乘得到特定积的乘法算式数量。需要注意的是,两个自然数相乘得到某一积时,这两个自然数是可以交换位置的,即不考虑顺序。
答案:积是12的乘法算式有:
$1 × 12 = 12$
$2 × 6 = 12$
$3 × 4 = 12$
$4 × 3 = 12$
$6 × 2 = 12$
$12 × 1 = 12$
答:积是12的乘法算式有6道。
答案:积是12的乘法算式有:
$1 × 12 = 12$
$2 × 6 = 12$
$3 × 4 = 12$
$4 × 3 = 12$
$6 × 2 = 12$
$12 × 1 = 12$
答:积是12的乘法算式有6道。
例题2 袋子里有红球、黄球、蓝球各两个,莎莎从袋子里任取两个球,一共有多少种不同的取法?
错误解法:红球、黄球 红球、蓝球 黄球、蓝球
答:一共有3种不同的取法。
正确解法:红球、黄球 红球、蓝球 黄球、蓝球 红球、红球 黄球、黄球 蓝球、蓝球
答:一共有6种不同的取法。
误点分析:错误解法错在遗漏了取颜色相同的两个球的情况。因为红球、黄球、蓝球各有两个,而不是各只有一个,所以取球时,还可能取出两个红球、两个黄球、两个蓝球。
错误解法:红球、黄球 红球、蓝球 黄球、蓝球
答:一共有3种不同的取法。
正确解法:红球、黄球 红球、蓝球 黄球、蓝球 红球、红球 黄球、黄球 蓝球、蓝球
答:一共有6种不同的取法。
误点分析:错误解法错在遗漏了取颜色相同的两个球的情况。因为红球、黄球、蓝球各有两个,而不是各只有一个,所以取球时,还可能取出两个红球、两个黄球、两个蓝球。
答案:
解析:本题考查的是用列举的策略解决实际问题。
需要从6个球(红球、黄球、蓝球各两个)中任取两个球,需要考虑所有可能的组合。
当从袋子里取两个球时,可能的组合有:
两个红球,
两个黄球,
两个蓝球,
一个红球和一个黄球,
一个红球和一个蓝球,
一个黄球和一个蓝球,
所以,一共有6种不同的取法。
答案:一共有6种不同的取法。
需要从6个球(红球、黄球、蓝球各两个)中任取两个球,需要考虑所有可能的组合。
当从袋子里取两个球时,可能的组合有:
两个红球,
两个黄球,
两个蓝球,
一个红球和一个黄球,
一个红球和一个蓝球,
一个黄球和一个蓝球,
所以,一共有6种不同的取法。
答案:一共有6种不同的取法。
查看更多完整答案,请扫码查看


