第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
例题3 一只蜗牛从点A出发,在一条直线上来回爬行。假设向右爬行的路程记为正数,向左爬行的路程记为负数,爬过的各段路程(单位:厘米)依次为+5、-3、+10、-6、-4、+7、-9。这只蜗牛最后是否回到了点A?
思路导引:从这只蜗牛的爬行情况看,记作正数的有+5、+10、+7,说明这只蜗牛一共向右爬行了5 + 10 + 7 = 22(厘米);记作负数的有-3、-6、-4、-9,说明这只蜗牛一共向左爬行了3 + 6 + 4 + 9 = 22(厘米)。因为这只蜗牛向右和向左都爬行了22厘米,所以这只蜗牛最后回到了点A。
完全解答:这只蜗牛最后回到了点A。
点评苑:解答此类问题时,关键看正数的和是否与负数去掉负号后的和相等,如果相等,就回到了出发点。
思路导引:从这只蜗牛的爬行情况看,记作正数的有+5、+10、+7,说明这只蜗牛一共向右爬行了5 + 10 + 7 = 22(厘米);记作负数的有-3、-6、-4、-9,说明这只蜗牛一共向左爬行了3 + 6 + 4 + 9 = 22(厘米)。因为这只蜗牛向右和向左都爬行了22厘米,所以这只蜗牛最后回到了点A。
完全解答:这只蜗牛最后回到了点A。
点评苑:解答此类问题时,关键看正数的和是否与负数去掉负号后的和相等,如果相等,就回到了出发点。
答案:
解析:本题考查正负数的实际应用和有理数的加法运算。通过计算蜗牛向右和向左爬行的总路程,判断其是否回到出发点。
将所有向右爬行的路程相加:
$+5+10+7=22$(厘米),
将所有向左爬行的路程(取绝对值后)相加:
$3+6+4+9=22$(厘米),
由于蜗牛向右爬行的总路程和向左爬行的总路程相等,即$22$厘米,因此蜗牛最后回到了出发点A。
答案:这只蜗牛最后回到了点A。
将所有向右爬行的路程相加:
$+5+10+7=22$(厘米),
将所有向左爬行的路程(取绝对值后)相加:
$3+6+4+9=22$(厘米),
由于蜗牛向右爬行的总路程和向左爬行的总路程相等,即$22$厘米,因此蜗牛最后回到了出发点A。
答案:这只蜗牛最后回到了点A。
1. +26读作(
正二十六
),-17读作(负十七
),负29记作(-29
)。
答案:
解析:本题主要考查正负数的读法和写法。在数学中,“+”读作正,“-”读作负,写数时直接用正负号加数字的形式表示。
答案: 正二十六;负十七;-29
答案: 正二十六;负十七;-29
2. 如图,下面是王亮某天的电子钱包账单,-77.00元表示(
|电子红包|+183.00元|
|XXX超市|-77.00元|
在XXX超市支出了77元
),这天电子钱包里增加了(106
)元。|电子红包|+183.00元|
|XXX超市|-77.00元|
答案:
解析:
首先,我们需要理解电子钱包账单中的正负号含义。在这个问题中,正数表示收入(即电子钱包里钱增加),负数表示支出(即电子钱包里钱减少)。
-77.00元出现在账单的“XXX超市”这一项,表示在XXX超市有77元的支出。
接下来,我们要计算这天电子钱包里总共增加了多少钱。
根据账单,王亮通过电子红包收入了183元,而在XXX超市支出了77元。
因此,这天电子钱包的净增加额为:$183 - 77 = 106(元)$。
答案:
-77.00元表示在XXX超市支出了77元;
这天电子钱包里增加了106元。
首先,我们需要理解电子钱包账单中的正负号含义。在这个问题中,正数表示收入(即电子钱包里钱增加),负数表示支出(即电子钱包里钱减少)。
-77.00元出现在账单的“XXX超市”这一项,表示在XXX超市有77元的支出。
接下来,我们要计算这天电子钱包里总共增加了多少钱。
根据账单,王亮通过电子红包收入了183元,而在XXX超市支出了77元。
因此,这天电子钱包的净增加额为:$183 - 77 = 106(元)$。
答案:
-77.00元表示在XXX超市支出了77元;
这天电子钱包里增加了106元。
|编号|1|2|3|4|
|质量/千克|47|50|49|51|
|超过(或不足)的质量/千克|
|编号|5|6|7|8|
|质量/千克|48|51|50|49|
|超过(或不足)的质量/千克|
若偏差不超过±1千克的视为合格,则合格的大米有(
|质量/千克|47|50|49|51|
|超过(或不足)的质量/千克|
-3
|0
|-1
|1
||编号|5|6|7|8|
|质量/千克|48|51|50|49|
|超过(或不足)的质量/千克|
-2
|1
|0
|-1
|若偏差不超过±1千克的视为合格,则合格的大米有(
6
)袋。
答案:
解析:本题考查正负数的实际应用以及简单的统计。主要涉及到如何根据给定的标准质量,计算每袋大米的超过或不足的质量,并统计合格的大米袋数。
首先,需要计算每袋大米相对于标准质量(50千克)的超过或不足的质量。这可以通过将每袋大米的质量减去标准质量来实现。
然后,需要统计偏差不超过±1千克的大米袋数,即合格的大米袋数。
编号1的大米质量为47千克,不足的质量为$47 - 50 = -3$(千克);
编号2的大米质量为50千克,与标准质量相同,所以不足或超过的质量为0千克;
编号3的大米质量为49千克,不足的质量为$49 - 50 = -1$(千克);
编号4的大米质量为51千克,超过的质量为$51 - 50 = 1$(千克);
编号5的大米质量为48千克,不足的质量为$48 - 50 = -2$(千克);
编号6的大米质量为51千克,超过的质量为$51 - 50 = 1$(千克);
编号7的大米质量为50千克,与标准质量相同,所以不足或超过的质量为0千克;
编号8的大米质量为49千克,不足的质量为$49 - 50 = -1$(千克)。
接下来,统计偏差不超过±1千克的大米袋数。这些大米袋的编号是:2、3、4、6、7、8,共有6袋。
答案:
|编号|1|2|3|4|
|----|----|----|----|----|
|质量/千克|47|50|49|51|
|超过(或不足)的质量/千克|-3|0|-1|1|
|编号|5|6|7|8|
|质量/千克|48|51|50|49|
|超过(或不足)的质量/千克|-2|1|0|-1|
合格的大米有6袋。
首先,需要计算每袋大米相对于标准质量(50千克)的超过或不足的质量。这可以通过将每袋大米的质量减去标准质量来实现。
然后,需要统计偏差不超过±1千克的大米袋数,即合格的大米袋数。
编号1的大米质量为47千克,不足的质量为$47 - 50 = -3$(千克);
编号2的大米质量为50千克,与标准质量相同,所以不足或超过的质量为0千克;
编号3的大米质量为49千克,不足的质量为$49 - 50 = -1$(千克);
编号4的大米质量为51千克,超过的质量为$51 - 50 = 1$(千克);
编号5的大米质量为48千克,不足的质量为$48 - 50 = -2$(千克);
编号6的大米质量为51千克,超过的质量为$51 - 50 = 1$(千克);
编号7的大米质量为50千克,与标准质量相同,所以不足或超过的质量为0千克;
编号8的大米质量为49千克,不足的质量为$49 - 50 = -1$(千克)。
接下来,统计偏差不超过±1千克的大米袋数。这些大米袋的编号是:2、3、4、6、7、8,共有6袋。
答案:
|编号|1|2|3|4|
|----|----|----|----|----|
|质量/千克|47|50|49|51|
|超过(或不足)的质量/千克|-3|0|-1|1|
|编号|5|6|7|8|
|质量/千克|48|51|50|49|
|超过(或不足)的质量/千克|-2|1|0|-1|
合格的大米有6袋。
4.
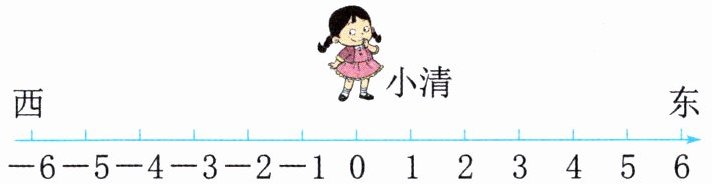
(1)小清从0点的位置向西走了5格,她走到了(

(1)小清从0点的位置向西走了5格,她走到了(
-5
)点的位置。(2)小东从3点的位置走到-2点的位置,是向(西
)走了(5
)格。(3)张明从1点的位置先向东走了3格,然后向西走了8格,他走到了(-4
)点的位置。
答案:
(1) 小清从0点的位置向西走了5格,由于向西走是负方向,因此她走到了$-5$点的位置。
答案:$-5$。
(2) 小东从3点的位置走到$-2$点的位置,由于3到-2是负方向,且距离是$3 - (-2) = 5$(格),因此他是向西走了5格。
答案:西;5。
(3) 张明从1点的位置先向东走了3格,位置变为$1 + 3 = 4$,然后向西走了8格,位置变为$4 - 8 = -4$,因此他走到了$-4$点的位置。
答案:$-4$。
(1) 小清从0点的位置向西走了5格,由于向西走是负方向,因此她走到了$-5$点的位置。
答案:$-5$。
(2) 小东从3点的位置走到$-2$点的位置,由于3到-2是负方向,且距离是$3 - (-2) = 5$(格),因此他是向西走了5格。
答案:西;5。
(3) 张明从1点的位置先向东走了3格,位置变为$1 + 3 = 4$,然后向西走了8格,位置变为$4 - 8 = -4$,因此他走到了$-4$点的位置。
答案:$-4$。
5. 一件衣服先按盈利50元定价销售,在季末清仓处理时,店主降价60元售出,这件衣服的盈利情况可以表示为(
-10元
)。
答案:
解析:本题考查加减法在实际问题中的应用,涉及到盈利和亏损的计算。
首先,衣服原本是按照盈利50元来定价的,所以初始盈利是+50元。
然后,在季末清仓处理时,店主降价60元售出,这实际上是一个亏损,因为降价金额超过了原本的盈利,所以要用负数来表示,即-60元。
最后的盈利情况就是这两部分的和,即$+50+(-60)=-10$(元)。
这表示店主在这件衣服上实际上亏损了10元。
答案:$-10$元。
首先,衣服原本是按照盈利50元来定价的,所以初始盈利是+50元。
然后,在季末清仓处理时,店主降价60元售出,这实际上是一个亏损,因为降价金额超过了原本的盈利,所以要用负数来表示,即-60元。
最后的盈利情况就是这两部分的和,即$+50+(-60)=-10$(元)。
这表示店主在这件衣服上实际上亏损了10元。
答案:$-10$元。
如图是四个城市在2025年1月某天的时间情况。以北京时间为标准,东京时间早1小时,记作+1时,伊斯兰堡时间记作(
-3
)时,伦敦时间记作(-8
)时。
答案:
解析:本题可根据所给城市时间与北京时间的早晚关系,结合正负数的表示方法来求解。
已知以北京时间为标准,东京时间早$1$小时,记作$ + 1$时,即比北京时间早的时间记为“$+$”,那么比北京时间晚的时间就记为“$-$”。
观察时钟可知,伊斯兰堡时间比北京时间晚$3$小时,所以伊斯兰堡时间记作$-3$时;
伦敦时间比北京时间晚$8$小时,所以伦敦时间记作$-8$时。
答案:$-3$;$-8$。
已知以北京时间为标准,东京时间早$1$小时,记作$ + 1$时,即比北京时间早的时间记为“$+$”,那么比北京时间晚的时间就记为“$-$”。
观察时钟可知,伊斯兰堡时间比北京时间晚$3$小时,所以伊斯兰堡时间记作$-3$时;
伦敦时间比北京时间晚$8$小时,所以伦敦时间记作$-8$时。
答案:$-3$;$-8$。
查看更多完整答案,请扫码查看


