2025年世超金典暑假乐园暑假八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年世超金典暑假乐园暑假八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2. 数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
|售价/(元/件)|100|110|120|130|…|
|月销量/件|200|180|160|140|…|
已知该运动服的进价为每件 60 元,设每件售价为 $ x (x ≥ 100) $ 元,则月销量是______
|售价/(元/件)|100|110|120|130|…|
|月销量/件|200|180|160|140|…|
已知该运动服的进价为每件 60 元,设每件售价为 $ x (x ≥ 100) $ 元,则月销量是______
$ -2x + 400 $
件,销售该运动服的月利润为______$ (x - 60)(-2x + 400) $(或 $ -2x^{2} + 520x - 24000 $)
元(用含 x 的式子表示).
答案:
2. $ -2x + 400 $ $ (x - 60)(-2x + 400) $(或 $ -2x^{2} + 520x - 24000 $)
某农庄计划在 30 亩(1 亩合 666.7 平方米)空地上全部种植蔬菜和水果,菜农小张和果农小李分别承包了种植蔬菜和水果的任务. 小张种植每亩蔬菜的工资 y(单位:元)与种植面积 m(单位:亩)之间的函数关系如图甲所示,小李种植水果所得报酬 z(单位:元)与种植面积 n(单位:亩)之间的函数关系如图乙所示.

(1)如果种植蔬菜 20 亩,则小张种植每亩蔬菜的工资是______
(2)当 $ 10 ≤ n ≤ 30 $ 时,求 z 与 n 之间的函数解析式;
(3)设农庄支付给小张和小李的总费用为 w(单位:元),当 $ 10 ≤ m ≤ 30 $ 时,求 w 与 m 之间的函数解析式.

(1)如果种植蔬菜 20 亩,则小张种植每亩蔬菜的工资是______
140
元,小张应得的工资总额是______2800
元,此时,小李种植水果______10
亩,小李应得的报酬是______1500
元;(2)当 $ 10 ≤ n ≤ 30 $ 时,求 z 与 n 之间的函数解析式;
(3)设农庄支付给小张和小李的总费用为 w(单位:元),当 $ 10 ≤ m ≤ 30 $ 时,求 w 与 m 之间的函数解析式.
答案:
解:
(1) 140 2800 10 1500
(2) 当 $ 10 \leq n \leq 30 $ 时,设 $ z $ 与 $ n $ 之间的函数解析式为 $ z = cn + d $,则有 $ \begin{cases} 10c + d = 1500, \\ 30c + d = 3900. \end{cases} $ 解得 $ \begin{cases} c = 120, \\ d = 300. \end{cases} $
即当 $ 10 \leq n \leq 30 $ 时,$ z $ 与 $ n $ 之间的函数解析式是 $ z = 120n + 300 $。
(3) 当 $ 10 \leq m \leq 30 $ 时,设题图甲所示函数为 $ y = kx + b $。
∵ 函数图象经过点 $ (10,160) $,$ (30,120) $,则有 $ \begin{cases} 10k + b = 160, \\ 30k + b = 120, \end{cases} $ 解得 $ \begin{cases} k = -2, \\ b = 180. \end{cases} $
$ \therefore $ 函数 $ y = -2x + 180 $。
当 $ 10 \leq m < 20 $ 时,$ 10 < n \leq 20 $,
$ \therefore w = m(-2m + 180) + 120(30 - m) + 300 = -2m^{2} + 60m + 3900 $。
当 $ 0 \leq n \leq 10 $ 时,设 $ z = b'n $,则 $ 10b' = 1500 $,得 $ b' = 150 $,即当 $ 0 \leq n \leq 10 $ 时,$ z = 150n $。
故当 $ 20 \leq m \leq 30 $ 时,$ 0 \leq n \leq 10 $,
$ w = m(-2m + 180) + 150(30 - m) = -2m^{2} + 30m + 4500 $。
由上可得 $ w = \begin{cases} -2m^{2} + 60m + 3900(10 \leq m < 20), \\ -2m^{2} + 30m + 4500(20 \leq m \leq 30). \end{cases} $
(1) 140 2800 10 1500
(2) 当 $ 10 \leq n \leq 30 $ 时,设 $ z $ 与 $ n $ 之间的函数解析式为 $ z = cn + d $,则有 $ \begin{cases} 10c + d = 1500, \\ 30c + d = 3900. \end{cases} $ 解得 $ \begin{cases} c = 120, \\ d = 300. \end{cases} $
即当 $ 10 \leq n \leq 30 $ 时,$ z $ 与 $ n $ 之间的函数解析式是 $ z = 120n + 300 $。
(3) 当 $ 10 \leq m \leq 30 $ 时,设题图甲所示函数为 $ y = kx + b $。
∵ 函数图象经过点 $ (10,160) $,$ (30,120) $,则有 $ \begin{cases} 10k + b = 160, \\ 30k + b = 120, \end{cases} $ 解得 $ \begin{cases} k = -2, \\ b = 180. \end{cases} $
$ \therefore $ 函数 $ y = -2x + 180 $。
当 $ 10 \leq m < 20 $ 时,$ 10 < n \leq 20 $,
$ \therefore w = m(-2m + 180) + 120(30 - m) + 300 = -2m^{2} + 60m + 3900 $。
当 $ 0 \leq n \leq 10 $ 时,设 $ z = b'n $,则 $ 10b' = 1500 $,得 $ b' = 150 $,即当 $ 0 \leq n \leq 10 $ 时,$ z = 150n $。
故当 $ 20 \leq m \leq 30 $ 时,$ 0 \leq n \leq 10 $,
$ w = m(-2m + 180) + 150(30 - m) = -2m^{2} + 30m + 4500 $。
由上可得 $ w = \begin{cases} -2m^{2} + 60m + 3900(10 \leq m < 20), \\ -2m^{2} + 30m + 4500(20 \leq m \leq 30). \end{cases} $
四、趣味题
将下面的木板分成 2 份,做成一个“+”字标志,请你来完成.

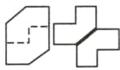
将下面的木板分成 2 份,做成一个“+”字标志,请你来完成.


答案:
如右图

如右图

查看更多完整答案,请扫码查看


