2025年世超金典暑假乐园暑假八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年世超金典暑假乐园暑假八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2. 在平行四边形$ABCD$中,点$O是边AD$的中点,连接$CO并延长交BA的延长线于点E$,连接$ED$,$AC$。
(1)如图甲,求证:四边形$AEDC$是平行四边形。
(2)如图乙,若四边形$AEDC$是矩形,请探究$∠COD与∠B$的数量关系,写出你的探究结论,并加以证明。
(1)证明:∵四边形ABCD是平行四边形,
∴AB//CD.
∴∠BEC=∠DCE.
∵点O是边AD的中点,
∴AO=DO.
又∵∠AOE=∠DOC,
∴△AEO≌△DCO(AAS).
∴AE=CD.
∴四边形AEDC是平行四边形.
(2)解:∠COD=
证明如下:∵四边形ABCD是平行四边形,
∴∠B=∠ADC.
∵四边形AEDC是矩形,
∴AO=EO=CO=DO.
∴∠ADC=∠OCD.
∵∠ADC+∠OCD+∠COD=180°,
∴∠COD=180°−2∠ADC=180°−2∠B.
(1)如图甲,求证:四边形$AEDC$是平行四边形。
(2)如图乙,若四边形$AEDC$是矩形,请探究$∠COD与∠B$的数量关系,写出你的探究结论,并加以证明。
(1)证明:∵四边形ABCD是平行四边形,
∴AB//CD.
∴∠BEC=∠DCE.
∵点O是边AD的中点,
∴AO=DO.
又∵∠AOE=∠DOC,
∴△AEO≌△DCO(AAS).
∴AE=CD.
∴四边形AEDC是平行四边形.
(2)解:∠COD=
180°−2∠B
.证明如下:∵四边形ABCD是平行四边形,
∴∠B=∠ADC.
∵四边形AEDC是矩形,
∴AO=EO=CO=DO.
∴∠ADC=∠OCD.
∵∠ADC+∠OCD+∠COD=180°,
∴∠COD=180°−2∠ADC=180°−2∠B.
答案:
(1)证明:
∵四边形ABCD是平行四边形,
∴AB//CD.
∴∠BEC=∠DCE.
∵点O是边AD的中点,
∴AO=DO.
又
∵∠AOE=∠DOC,
∴△AEO≌△DCO(AAS).
∴AE=CD.
∴四边形AEDC是平行四边形.
(2)解:∠COD=180°−2∠B.
证明如下:
∵四边形ABCD是平行四边形,
∴∠B=∠ADC.
∵四边形AEDC是矩形,
∴AO=EO=CO=DO.
∴∠ADC=∠OCD.
∵∠ADC+∠OCD+∠COD=180°,
∴∠COD=180°−2∠ADC=180°−2∠B.
(1)证明:
∵四边形ABCD是平行四边形,
∴AB//CD.
∴∠BEC=∠DCE.
∵点O是边AD的中点,
∴AO=DO.
又
∵∠AOE=∠DOC,
∴△AEO≌△DCO(AAS).
∴AE=CD.
∴四边形AEDC是平行四边形.
(2)解:∠COD=180°−2∠B.
证明如下:
∵四边形ABCD是平行四边形,
∴∠B=∠ADC.
∵四边形AEDC是矩形,
∴AO=EO=CO=DO.
∴∠ADC=∠OCD.
∵∠ADC+∠OCD+∠COD=180°,
∴∠COD=180°−2∠ADC=180°−2∠B.
3. 如图,过矩形$ABCD的对角线AC的中点O作EF⊥AC$,交$BC边于点E$,交$AD边于点F$,分别连接$AE$,$CF$。
(1)求证:四边形$AECF$是菱形。
(2)若$AB= 3$,$∠DCF= 30^{\circ}$,求$EF$的长。
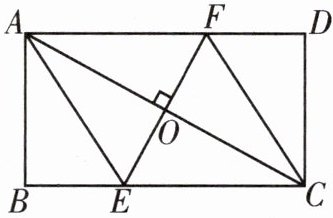
(1)证明:∵四边形ABCD是矩形,
∴∠FAO=∠ECO,AO=CO.
在△AOF与△COE中,
$\left\{\begin{array}{l}\angle FAO = \angle ECO,\\AO = CO,\\\angle AOF = \angle COE\end{array}\right.$
∴△AOF≌△COE(ASA).
∴OF=OE.
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴四边形AECF是菱形.
(2)解:∵∠DCF=30°,AB=CD=3,
∴∠FCE=60°,CF²=($\frac{1}{2}$CF)²+3².
∴CF=2√3.
∵CF=CE,∴△EFC是等边三角形
∴EF=
(1)求证:四边形$AECF$是菱形。
(2)若$AB= 3$,$∠DCF= 30^{\circ}$,求$EF$的长。

(1)证明:∵四边形ABCD是矩形,
∴∠FAO=∠ECO,AO=CO.
在△AOF与△COE中,
$\left\{\begin{array}{l}\angle FAO = \angle ECO,\\AO = CO,\\\angle AOF = \angle COE\end{array}\right.$
∴△AOF≌△COE(ASA).
∴OF=OE.
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴四边形AECF是菱形.
(2)解:∵∠DCF=30°,AB=CD=3,
∴∠FCE=60°,CF²=($\frac{1}{2}$CF)²+3².
∴CF=2√3.
∵CF=CE,∴△EFC是等边三角形
∴EF=
2√3
答案:
(1)证明:
∵四边形ABCD是矩形,
∴∠FAO=∠ECO,AO=CO.
在△AOF与△COE中,
$\left\{\begin{array}{l}\angle FAO = \angle ECO,\\AO = CO,\\\angle AOF = \angle COE\end{array}\right.$
∴△AOF≌△COE(ASA).
∴OF=OE.
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴四边形AECF是菱形.
(2)解:
∵∠DCF=30°,AB=CD=3,
∴∠FCE=60°,CF²=($\frac{1}{2}$CF)²+3².
∴CF=2√3.
∵CF=CE,
∴△EFC是等边三角形
∴EF=2$\sqrt{3}$
(1)证明:
∵四边形ABCD是矩形,
∴∠FAO=∠ECO,AO=CO.
在△AOF与△COE中,
$\left\{\begin{array}{l}\angle FAO = \angle ECO,\\AO = CO,\\\angle AOF = \angle COE\end{array}\right.$
∴△AOF≌△COE(ASA).
∴OF=OE.
∴四边形AECF是平行四边形.
∵EF⊥AC,
∴四边形AECF是菱形.
(2)解:
∵∠DCF=30°,AB=CD=3,
∴∠FCE=60°,CF²=($\frac{1}{2}$CF)²+3².
∴CF=2√3.
∵CF=CE,
∴△EFC是等边三角形
∴EF=2$\sqrt{3}$
4. 如图,在$Rt\triangle ABC$中,$∠C= 90^{\circ}$,$M是AB$的中点,$AM= AN$,$MN// AC$。
(1)求证:$MN= AC$。
(2)如果把条件“$AM= AN$”改为“$AM⊥AN$”,其他条件不变,那么$MN= AC$不一定成立。如果再改变一个条件,就能使$MN= AC$成立。请你写出改变的条件并说明理由。
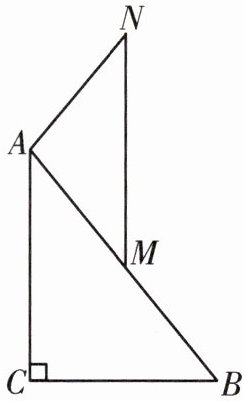
(1)证明:连接CM,则AM=CM,∠MAC=∠MCA.又∵MN//AC,
∴∠NMA=∠MAC.
∴∠ANM=∠NMA=∠MAC=∠MCA.
又∵AM为公共边,
∴△AMN≌△MAC.∴MN=AC.
(2)解:改变的条件是
理由:∵AC=BC,∠C=90°,∴∠CMA=90°.
同理可证△AMN≌△MAC.∴MN=AC.
(1)求证:$MN= AC$。
(2)如果把条件“$AM= AN$”改为“$AM⊥AN$”,其他条件不变,那么$MN= AC$不一定成立。如果再改变一个条件,就能使$MN= AC$成立。请你写出改变的条件并说明理由。

(1)证明:连接CM,则AM=CM,∠MAC=∠MCA.又∵MN//AC,
∴∠NMA=∠MAC.
∴∠ANM=∠NMA=∠MAC=∠MCA.
又∵AM为公共边,
∴△AMN≌△MAC.∴MN=AC.
(2)解:改变的条件是
AC=BC
。理由:∵AC=BC,∠C=90°,∴∠CMA=90°.
同理可证△AMN≌△MAC.∴MN=AC.
答案:
(1)证明:连接CM,则AM=CM,∠MAC=∠MCA.又
∵MN//AC,
∴∠NMA=∠MAC.
∴∠ANM=∠NMA=∠MAC=∠MCA.
又
∵AM为公共边,
∴△AMN≌△MAC.
∴MN=AC.
(2)解:AC=BC.
理由:
∵AC=BC,∠C=90°,
∴∠CMA=90°.
同理可证△AMN≌△MAC.
∴MN=AC.
(1)证明:连接CM,则AM=CM,∠MAC=∠MCA.又
∵MN//AC,
∴∠NMA=∠MAC.
∴∠ANM=∠NMA=∠MAC=∠MCA.
又
∵AM为公共边,
∴△AMN≌△MAC.
∴MN=AC.
(2)解:AC=BC.
理由:
∵AC=BC,∠C=90°,
∴∠CMA=90°.
同理可证△AMN≌△MAC.
∴MN=AC.
四、趣味题
在不能重复的情况下,你能一笔把下面的图形画出来吗?
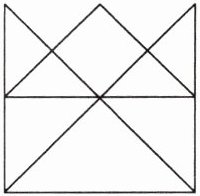
在不能重复的情况下,你能一笔把下面的图形画出来吗?

能
答案:
【解析】:根据一笔画定理,判断一个图形能否一笔画成,关键在于数出图形中奇点(与奇数条边相连的点)的个数。此图形中奇点个数为$2$个。
【答案】:能。
【答案】:能。
查看更多完整答案,请扫码查看


