《2025年世超金典暑假乐园暑假八年级数学人教版》

1. 若a,b,c为三角形的三边长,则$\sqrt {(a-b-c)^{2}}= $b + c - a.

答案： 1. $ b + c - a $

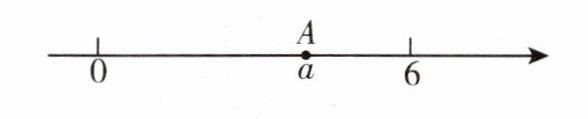
2. 如图,数轴上点A表示的数为a,化简:$a+\sqrt {a^{2}-12a+36}= $6.

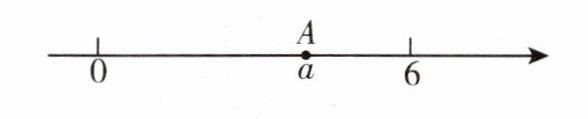
答案： 2. 6

3.$\sqrt {0.0004}= $0.02.

答案： 3. 0.02

4. 已知$a≥0$时,$\sqrt {a^{2}}= a$.请你根据这个结论直接填空:
(1)$\sqrt {9}= $3;(2)若$x+1= 2018^{2}+2019^{2}$,则$\sqrt {2x+1}= $4 037.

答案： 4.
(1)3
(2)4 037

1. 某工厂要制作一批体积为$1m^{3}$的产品包装盒,其高为0.2m,按设计需要,底面应做成正方形,底面边长应是多少?

答案： 1. $ \sqrt { 5 } $ m

2. 阅读材料:
小明在学习二次根式的化简后,遇到了这样一个需要化简的式子:$\sqrt {3+2\sqrt {2}}$.该如何化简呢?思考后,他发现$3+2\sqrt {2}= 1+2\sqrt {2}+(\sqrt {2})^{2}= (1+\sqrt {2})^{2}$.于是$\sqrt {3+2\sqrt {2}}= \sqrt {(1+\sqrt {2})^{2}}= 1+\sqrt {2}$.善于思考的小明继续深入探索,当$a+b\sqrt {2}= (m+n\sqrt {2})^{2}$(其中a,b,m,n均为正整数)时,$a+b\sqrt {2}= m^{2}+2\sqrt {2}mn+2n^{2}$.此时$a= m^{2}+2n^{2},b= 2mn$.于是$\sqrt {a+b\sqrt {2}}= m+n\sqrt {2}$.请你仿照小明的方法探索并解决下列问题:
(1)设a,b,m,n均为正整数,且$\sqrt {a+b\sqrt {3}}= m+n\sqrt {3}$,用含m,n的式子分别表示a,b,结果是$a= $$ m ^ { 2 } + 3 n ^ { 2 } $,$b= $2mn.
(2)利用(1)中的结论,选择一组正整数填空:$\sqrt {(7)+(4)\sqrt {3}}= $2+1$\sqrt {3}$.(答案不唯一)
(3)化简:$\sqrt {6+2\sqrt {5}}$.

答案： 2.
(1)$ m ^ { 2 } + 3 n ^ { 2 } $ 2mn
(2)7 4 2 1(答案不唯一)
(3)$ \sqrt { 6 + 2 \sqrt { 5 } } = \sqrt { ( \sqrt { 5 } + 1 ) ^ { 2 } } = \sqrt { 5 } + 1 $

四、趣味题
你能在下图中找出不符合排列规律的图形吗?

C 排列规律是小圆圈的数量等于多边形的边数.

答案： 四、C 排列规律是小圆圈的数量等于多边形的边数.