《2025年世超金典暑假乐园暑假八年级数学人教版》

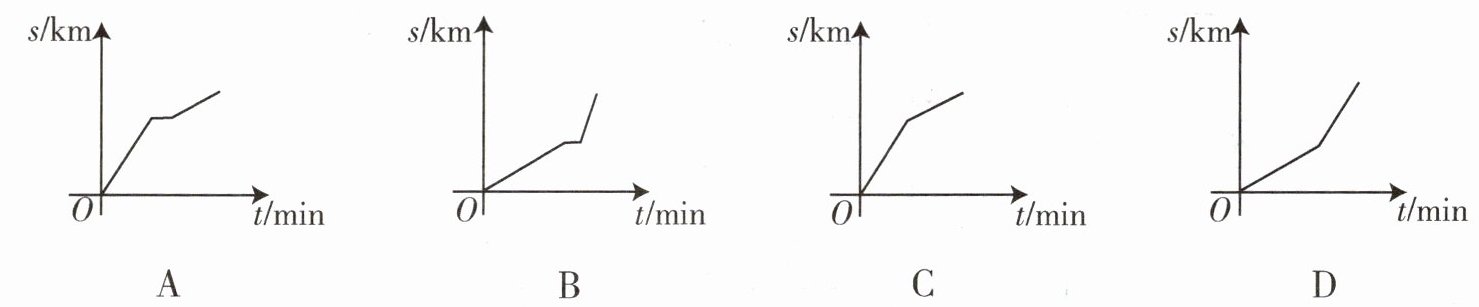
3. 某教师到一村寨进行学生家访工作,开始时骑摩托车大约用了40 min的时间走了10 km,休息了10 min,然后花近30 min的时间徒步走了4 km到达该村寨. 下列能表示该教师行走的路程$s$(单位：km)与时间$t$(单位：min)的函数关系的图象是(A)

答案： 3.A

4. 有下列函数：①$y = 2x - 1$；②$y = -\frac{x}{2}$；③$y = \frac{1}{x}$；④$y = 2^{-1} - x$；⑤$y = x^2$. 其中一次函数有(C)

A.1个
B.2个
C.3个
D.4个

答案： 4.C

5. 直线$y = -3x + 2$不经过的象限是(C)

A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： 5.C

6. 直线$y = -2x + b$与两坐标轴围成的三角形的面积为4,则$b$的值为(C)

A.4
B.-4
C.±4
D.±2

答案： 6.C

1. 已知有理数$x$,$y满足2x - 3y = 4$,并且$x \geq -1$,$y ＜ 2$. 现有$k = x - y$,则$k$的最小值是______1.

答案： 1. 首先，由$2x - 3y = 4$得$x=\frac{4 + 3y}{2}$：
因为$x\geq - 1$，所以$\frac{4 + 3y}{2}\geq - 1$。
解不等式$\frac{4 + 3y}{2}\geq - 1$：
两边同时乘以$2$得$4 + 3y\geq - 2$。
移项得$3y\geq - 2 - 4$，即$3y\geq - 6$，解得$y\geq - 2$。
又因为$y\lt2$，所以$-2\leq y\lt2$。
2. 然后，将$k = x - y$进行变形：
把$x=\frac{4 + 3y}{2}$代入$k = x - y$中，$k=\frac{4 + 3y}{2}-y$。
化简$k=\frac{4 + 3y}{2}-y=\frac{4 + 3y-2y}{2}=\frac{4 + y}{2}$。
3. 最后，求$k$的最小值：
因为$k=\frac{4 + y}{2}$，$y$的取值范围是$-2\leq y\lt2$，$k$随$y$的增大而增大。
当$y=-2$时，$k$取得最小值。
把$y = - 2$代入$k=\frac{4 + y}{2}$，则$k=\frac{4+( - 2)}{2}$。
根据有理数除法法则$\frac{4+( - 2)}{2}=\frac{2}{2}=1$。
所以$k$的最小值是$1$。

2. 函数$y = (m + 3)x^{m^2 - 8} - 5$是一次函数,则$m$的值是______3.

答案： 2.3

3. 若一次函数$y = ax + 1 - a$中,$y随x$的增大而增大,且它的图象与$y$轴交于正半轴,则$|a - 1| + \sqrt{a^2} = $______1.

答案： 3.1

(1)求$S$关于$x$的函数解析式为$S=20-4x$，$x$的取值范围是$0。
(2)当$S = 10$时，点$P$的坐标是

$(2.5,2.5)$

。

答案： 解:
(1)由 $ x + y = 5 $ 得 $ y = 5 - x $。
在第一象限内过点 $ P(x, y) $ 作 $ PE \perp x $ 轴于点 $ E $，则 $ PE = y $，$ x ＞ 0 $，$ y ＞ 0 $。
$\therefore S = \frac{1}{2}OA \cdot PE = \frac{1}{2} × 8 × y = 4(5 - x) = 20 - 4x$。
$\therefore$ 由 $ y = 5 - x ＞ 0 $ 得 $ x ＜ 5 $。
$\therefore x$ 的取值范围是 $ 0 ＜ x ＜ 5 $。
(2)当 $ S = 10 $ 时，由 $ 10 = 20 - 4x $ 得 $ x = 2.5 $。
$\therefore$ 点 $ P $ 的坐标是 $ (2.5, 2.5) $。

四、趣味题
如图所示,有4个三角形,你能再添加一个三角形,使之变成14个三角形吗？

答案：
能，再加一个大三角形(如下图).

四、趣味题
如图所示,有4个三角形,你能再添加一个三角形,使之变成14个三角形吗？

答案：
能，再加一个大三角形(如下图).