《2025年世超金典暑假乐园暑假八年级数学人教版》

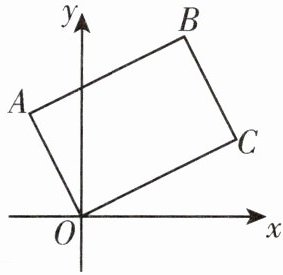
2. 将矩形 $OABC$ 如图放置在平面直角坐标系中,$O$ 为原点,若点 $A$ 的坐标是 $(-1,2)$,点 $B$ 的坐标是 $(2,\frac{7}{2})$,则点 $C$ 的坐标是 (D)

A.$(4,2)$
B.$(2,4)$
C.$(\frac{3}{2},3)$
D.$(3,\frac{3}{2})$

答案： D

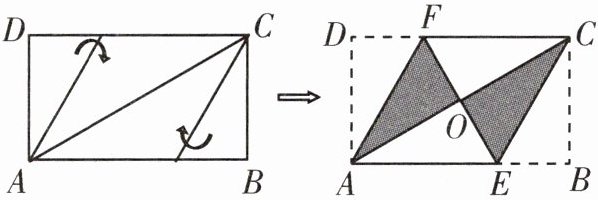
3. 将矩形纸片 $ABCD$ 按如图所示的方式折叠,得到菱形 $AECF$. 若 $AB= 3$,则 $BC$ 的长为 (D)

A.1
B.2
C.$\sqrt{2}$
D.$\sqrt{3}$

答案： D

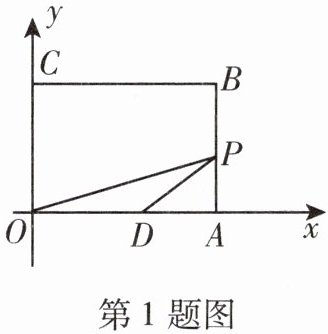
1. 如图,矩形 $OABC$ 的顶点 $A,C$ 分别在坐标轴上,$B(8,7),D(5,0)$,点 $P$ 是边 $AB$ 或边 $BC$ 上的一点,连接 $OP,DP$,当 $\triangle ODP$ 为等腰三角形时,点 $P$ 的坐标为 ______$(8,4)$或$(\frac {5}{2},7)$.

答案： $(8,4)$或$(\frac {5}{2},7)$

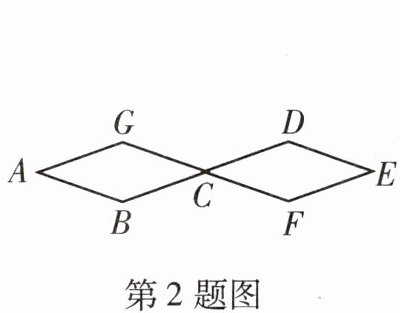
2. 如图所示,两个全等菱形的边长为 $1 cm$,一只蚂蚁由点 $A$ 开始按 $ABCDEFCGA$ 的顺序沿菱形的边循环运动,行走 $2024 cm$ 后停下,则这只蚂蚁停在 ______A点.

答案： A

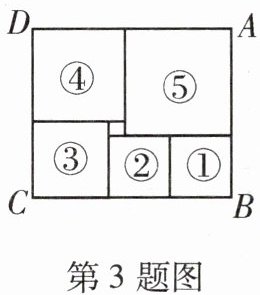
3. 如图是电脑屏幕上出现的一幅矩形色块图,由 $6$ 个颜色不同的正方形组成,设中间最小的一个正方形边长为 $1$,则这个矩形色块图的面积为 ______143.

答案： 143

(1)求证:四边形 MANP 是正方形.
证明：∵ 四边形 ABCD 是正方形，
$\therefore ∠DAB=90^{\circ }$，AC 平分$∠DAB$。
$\because PM⊥AD,PN⊥AB$，
$\therefore ∠PMA=∠PNA=90^{\circ }$。∴ 四边形 MANP 是矩形。
∵ AC 平分$∠DAB,PM⊥AD,PN⊥AB$，
$\therefore PM=PN$。∴ 四边形 MANP 是正方形。
(2)求证:$EM= BN$。
证明：∵ 四边形 MANP 是正方形，
$\therefore ∠MPN=90^{\circ }$。
$\because ∠EPB=90^{\circ }$，
$\therefore ∠MPE+∠EPN=∠NPB+∠EPN=90^{\circ }$。
$\therefore ∠MPE=∠NPB$。
在$△EPM$和$△BPN$中，
$\left\{\begin{array}{l} ∠PME=∠PNB=90^{\circ },\\ PM=PN,\\ ∠MPE=∠NPB,\end{array}\right. $
$\therefore △EPM\cong △BPN(ASA)$。
$\therefore EM=BN$。

答案： 证明：
(1)
∵ 四边形 ABCD 是正方形，
$\therefore ∠DAB=90^{\circ }$，AC 平分$∠DAB$。
$\because PM⊥AD,PN⊥AB$，
$\therefore ∠PMA=∠PNA=90^{\circ }$。
∴ 四边形 MANP 是矩形。
∵ AC 平分$∠DAB,PM⊥AD,PN⊥AB$，
$\therefore PM=PN$。
∴ 四边形 MANP 是正方形。
(2)
∵ 四边形 MANP 是正方形，
$\therefore ∠MPN=90^{\circ }$。
$\because ∠EPB=90^{\circ }$，
$\therefore ∠MPE+∠EPN=∠NPB+∠EPN=90^{\circ }$。
$\therefore ∠MPE=∠NPB$。
在$△EPM$和$△BPN$中，
$\left\{\begin{array}{l} ∠PME=∠PNB=90^{\circ },\\ PM=PN,\\ ∠MPE=∠NPB,\end{array}\right. $
$\therefore △EPM\cong △BPN(ASA)$。
$\therefore EM=BN$。