《2025年世超金典暑假乐园暑假八年级数学人教版》

4. 如图,在$△ABC$中,$∠B= ∠C$,AD平分$∠BAC$,若$AB= 5,BC= 6$,则$AD= $____4__.

答案： 4

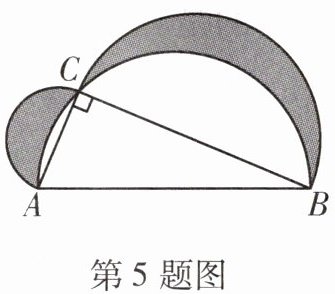
5. 如图,在$Rt△ABC$中,$∠C= 90^{\circ }$,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”.当$AC= 5,BC= 12$时,阴影部分的面积为____30__.

答案： 30

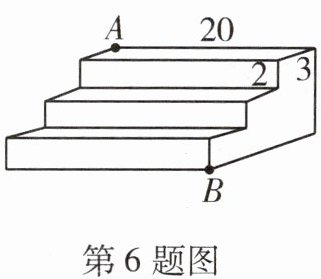
6. 如图是一个三级台阶,它的每一级的长、宽、高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是____25 dm__.

答案： 25 dm

7. 一艘小船早晨$8:00$出发,它以8海里/时的速度向东航行,1小时后,另一艘小船从同一出发地点以12海里/时的速度向南航行,上午$10:00$,两小船相距____20__海里.

答案： 20

1. 如图,在$△ABC$中,$AB= 5,AC= 4,∠A= 60^{\circ }$,若边AC的垂直平分线DE交AB于点D,交AC于点E,连接CD,求:
(1)BC的长;$\sqrt{21}$
(2)$△BDC$的周长.$5+\sqrt{21}$

答案： 解:
(1)过点 C 作 $CM\perp AB$,垂足为 M.
在 $Rt\triangle AMC$ 中,$\because \angle A=60^{\circ},AC=4$,
$\therefore AM=2,MC=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$.
$\therefore BM=AB-AM=5-2=3$.
在 $Rt\triangle BMC$ 中,
$BC=\sqrt{BM^{2}+CM^{2}}=\sqrt{3^{2}+(2\sqrt{3})^{2}}=\sqrt{21}$.
(2)$\because DE$ 是线段 $AC$ 的垂直平分线,
$\therefore AD=DC$.
又 $\because \angle A=60^{\circ}$,
$\therefore \triangle ADC$ 是等边三角形.
$\therefore CD=AD=AC=4$.
$\therefore \triangle BDC$ 的周长为 $DB+DC+BC=AD+DB+BC=AB+BC=5+\sqrt{21}$.
即 $\triangle BDC$ 的周长是 $5+\sqrt{21}$.

2. 如图,在$△ABC$中,$AC= 9,AB= 12,BC= 15$,AD是BC边上的高.
(1)求证:$△ABC$是直角三角形.
证明:$\because AC=9,AB=12,BC=15$,
$\therefore AC^{2}=81,AB^{2}=144,BC^{2}=225$.
$\therefore AC^{2}+AB^{2}=BC^{2}$.
$\therefore \angle BAC=90^{\circ}$.
$\therefore \triangle ABC$ 是直角三角形.
(2)求AD的长.
解:$\because S_{\triangle ABC}=\frac{1}{2}AB\cdot AC=\frac{1}{2}BC\cdot AD$,
$\therefore AD=\frac{AB\cdot AC}{BC}=$$\frac{36}{5}$.

答案：
(1)证明:$\because AC=9,AB=12,BC=15$,
$\therefore AC^{2}=81,AB^{2}=144,BC^{2}=225$.
$\therefore AC^{2}+AB^{2}=BC^{2}$.
$\therefore \angle BAC=90^{\circ}$.
$\therefore \triangle ABC$ 是直角三角形.
(2)解:$\because S_{\triangle ABC}=\frac{1}{2}AB\cdot AC=\frac{1}{2}BC\cdot AD$,
$\therefore AD=\frac{AB\cdot AC}{BC}=\frac{36}{5}$.