《2025年世超金典暑假乐园暑假八年级数学人教版》

4. 如下图,有一个由传感器控制的灯 $ A $,要装在门上方离地面 $ 4.5 \mathrm{~m} $ 的墙上,任何东西只要移至该灯 $ 5 \mathrm{~m} $ 及 $ 5 \mathrm{~m} $ 内,灯就会自动发光. 小明身高 $ 1.5 \mathrm{~m} $,他走到离墙4 m的地方灯刚好发光.

答案： 4 m

1. 每个正方形中的数字表示的是所在正方形的面积,求图中字母所代表的正方形面积.

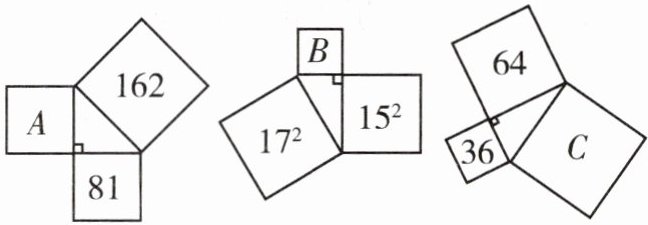
正方形A的面积为81，正方形B的面积为64，正方形C的面积为100。

答案： 求正方形$A$的面积
解：根据勾股定理，若直角三角形的两条直角边边长分别为$a$、$b$，斜边边长为$c$，则$a^{2}+b^{2}=c^{2}$。
在以正方形$A$、面积为$81$的正方形的边长为直角边，面积为$162$的正方形的边长为斜边的直角三角形中，设正方形$A$的面积为$S_{A}$，已知面积为$81$的正方形面积$S_{1}=81$，面积为$162$的正方形面积$S_{2}=162$。
由勾股定理的几何意义（以直角三角形三边为边长的正方形面积关系：两直角边所对应的正方形面积之和等于斜边所对应的正方形面积）可得$S_{A}+S_{1}=S_{2}$，即$S_{A}+81 = 162$，解得$S_{A}=162 - 81=81$。
求正方形$B$的面积
解：设正方形$B$的面积为$S_{B}$，已知$17^{2}=289$，$15^{2}=225$。
根据勾股定理的几何意义可得$S_{B}+15^{2}=17^{2}$，即$S_{B}+225 = 289$，解得$S_{B}=289 - 225 = 64$。
求正方形$C$的面积
解：设正方形$C$的面积为$S_{C}$，已知$64$和$36$。
根据勾股定理的几何意义可得$64+36=S_{C}$，解得$S_{C}=100$。
综上，正方形$A$的面积为$\boldsymbol{81}$，正方形$B$的面积为$\boldsymbol{64}$，正方形$C$的面积为$\boldsymbol{100}$。

2. 如图所示,一架梯子 $ A B $ 斜靠在墙面上,且 $ A B $ 的长为 $ 2.5 \mathrm{~m} $.
(1)若梯子底端离墙角的距离 $ O B $ 为 $ 0.7 \mathrm{~m} $,求这个梯子的顶端 $ A $ 距地面有多高.2.4m
(2)在(1)的条件下,如果梯子的顶端 $ A $ 下滑 $ 0.4 \mathrm{~m} $ 到点 $ A^{\prime} $,那么梯子的底端 $ B $ 在水平方向滑动的距离 $ B B^{\prime} $ 为多少米?0.8m

答案： 解：
(1) 根据勾股定理，梯子顶端 A 距离地面的高度
$AO = \sqrt{AB^{2} - OB^{2}} = \sqrt{2.5^{2} - 0.7^{2}} = 2.4(m)$.
(2) 梯子下滑了 0.4 m，即梯子顶端 $A'$ 距离地面的高度
$OA' = 2.4 - 0.4 = 2(m)$.
根据勾股定理，$OB' = \sqrt{A'B'^{2} - OA'^{2}} = 1.5(m)$，
∴ 当梯子的顶端下滑 0.4 m 时，梯子的底端 B 在水平方向滑动的距离 $BB' = 1.5 - 0.7 = 0.8(m)$.

四、趣味题
如图,直线 $ l $ 上有三个正方形 $ a,b,c $,若 $ a,c $ 的面积分别为 5 和 11 ,则 $ b $ 的面积为 (C)


A.4
B.6
C.16
D.55

答案： C