《2025年世超金典暑假乐园暑假八年级数学人教版》

3. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,且$2a = 3b$,$c = 2\sqrt{13}$,则$a = $6,$b = $4。

答案： 6 4

4. 在$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,$AB = 3$,$BC = 4$,过点B的直线把$\triangle ABC$分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是3.6 或 4.32 或 4.8。

答案： 3.6 或 4.32 或 4.8

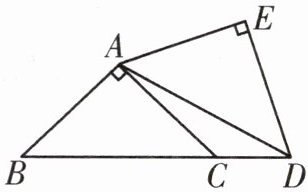
5. 把两个同样大小的含$45^{\circ}$角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上。若$AB = \sqrt{2}$,则$CD = $$\sqrt{3}-1$。

答案： $\sqrt{3}-1$

1. 已知$Rt\triangle ABC$的两条直角边分别为a和b,斜边为c,斜边上的高为h。判断以h,$c + h$,$a + b$为边的三角形的形状。

答案： 解：由已知得 $a^{2}+b^{2}=c^{2}$，$hc=ab$。
$\because (a+b)^{2}=a^{2}+b^{2}+2ab=c^{2}+2ab=c^{2}+2hc$，
$(c+h)^{2}=c^{2}+2ch+h^{2}=(a+b)^{2}+h^{2}$，
$\therefore (a+b)^{2}+h^{2}=(c+h)^{2}$。
即以 $h$，$c+h$，$a+b$ 为边的三角形是直角三角形。

2. 如图,沿AC方向开山修路。为了加快施工进度,要在小山的另一边同时施工。在AC上取一点B,且$\angle ABD = 120^{\circ}$,$BD = 520m$,$\angle D = 30^{\circ}$。那么另一边开挖点E离点D多远正好使A,C,E三点在一条直线上？($\sqrt{3}$取1.732,结果取整数)

450

答案： 解：因为$A$、$C$、$E$三点在一条直线上，$\angle ABD = 120^{\circ}$，所以$\angle EBD=180^{\circ}-\angle ABD = 60^{\circ}$。
又因为$\angle D = 30^{\circ}$，根据三角形内角和为$180^{\circ}$，可得$\angle BED = 180^{\circ}-\angle EBD-\angle D=180^{\circ}- 60^{\circ}-30^{\circ}=90^{\circ}$。
在$Rt\triangle BDE$中，$\angle D = 30^{\circ}$，$BD = 520m$。
根据直角三角形中$30^{\circ}$所对的直角边等于斜边的一半，可得$BE=\frac{1}{2}BD = 260m$。
再根据勾股定理$DE=\sqrt{BD^{2}-BE^{2}}$，将$BD = 520m$，$BE = 260m$代入可得：
$DE=\sqrt{520^{2}-260^{2}}=\sqrt{(520 + 260)(520 - 260)}=\sqrt{780×260}=\sqrt{202800}=260\sqrt{3}$
已知$\sqrt{3}\approx1.732$，则$DE\approx260×1.732 = 450.32\approx450m$。
所以另一边开挖点$E$离点$D$约$450m$正好使$A$，$C$，$E$三点在一条直线上。