《2025年世超金典暑假乐园暑假八年级数学人教版》

5. 下面说法正确的是 (D)

A.在 $Rt\triangle ABC$ 中,$a^{2}+b^{2}= c^{2}$
B.在 $Rt\triangle ABC$ 中,如果 $a= 3,b= 4$,那么 $c= 5$
C.直角三角形两直角边长都是 5,那么斜边长为 10
D.直角三角形中,斜边最长

答案： D

1. 已知直角三角形的三边长分别为 $5,12,13$,则斜边上的高等于____\frac{60}{13}.

答案： $\frac{60}{13}$

2. 有两棵树,一棵高 $6m$,另一棵高 $3m$,两树相距 $4m$,一只小鸟从一棵树的树梢飞到另一棵树的树梢至少要飞____5m.

答案： 5

3. 利用图甲或图乙两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理,这个定理称为____勾股定理,该定理的结论的数学表达式是____$a^{2}+b^{2}=c^{2}$.

答案： 勾股定理 $a^{2}+b^{2}=c^{2}$

4. 我国古代数学家赵爽的“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是 13,小正方形的面积是 1,直角三角形的两直角边长分别为 $a,b$,那么 $(a+b)^{2}$ 的值是____25.

答案： 25

三、解答题
小强家有一块三角形菜地,量得两边长分别为 $40m,50m$,第三边上的高为 $30m$,请你帮小强计算一下这块菜地的面积(结果保留根号).

答案： 解：设$AB = 40m$，$AC = 50m$，$AD$为第三边上的高，$AD = 30m$。
分两种情况：
情况一：当$\angle B$，$\angle C$均为锐角时：
在$Rt\triangle ABD$中，根据勾股定理$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{40^{2}-30^{2}}=\sqrt{1600 - 900}=\sqrt{700}=10\sqrt{7}(m)$
在$Rt\triangle ACD$中，根据勾股定理$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{50^{2}-30^{2}}=\sqrt{2500 - 900}=\sqrt{1600}=40(m)$
所以$BC=BD + CD=(10\sqrt{7}+40)m$
此时三角形面积$S=\dfrac{1}{2}BC\cdot AD=\dfrac{1}{2}(10\sqrt{7}+40)×30=(150\sqrt{7}+600)(m^{2})$
情况二：当$\angle B$为锐角，$\angle ACB$为钝角时：
在$Rt\triangle ABD$中，$BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{40^{2}-30^{2}}=10\sqrt{7}(m)$
在$Rt\triangle ACD$中，$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{50^{2}-30^{2}} = 40(m)$
所以$BC=CD - BD=(40 - 10\sqrt{7})m$
此时三角形面积$S=\dfrac{1}{2}BC\cdot AD=\dfrac{1}{2}(40 - 10\sqrt{7})×30=(600 - 150\sqrt{7})(m^{2})$
综上，这块菜地的面积为$(150\sqrt{7}+600)m^{2}$或$(600 - 150\sqrt{7})m^{2}$。

四、趣味题
如图,我国古代数学中有这样一道数学题:有一棵树直立在地上,树干高 2 丈,粗 3 尺,有一根藤条从树根缠绕而上,正好缠绕 7 周到树干顶部,请问这根藤条有多长? (注:树可以看成圆柱;树粗 3 尺,指的是圆柱底面圆周长为 3 尺.1 丈 $=10$ 尺)

答案：
解：将树干的侧面包括藤条一次展开，可以得到如图所示的图形，显然 $AB = 20$ 尺，$BC_{1} = 3$ 尺，$BC_{7} = 21$ 尺。

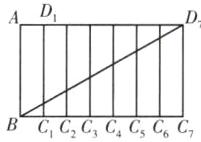
在 $Rt\triangle BC_{7}D_{7}$ 中，
∵ $\angle BC_{7}D_{7} = 90^{\circ}$，
∴ $BD_{7}^{2} = BC_{7}^{2} + C_{7}D_{7}^{2}$。
即 $BD_{7}^{2} = 20^{2} + 21^{2}$。
∴ $BD_{7} = 29$（尺）。
∴ 这根藤条长 29 尺。