《2025年世超金典暑假乐园暑假八年级数学人教版》

4. 如图,$ AC⊥CE,AD = BE = 13,BC = 5,DE = 7 $,那么$ AC = $12.

答案： 4. 12

5. 勾股定理中的$ a^{2} + b^{2} = c^{2} $本身就是一个关于a,b,c的方程,满足这个方程的正整数解(a,b,c)通常叫做勾股数组. 毕达哥拉斯学派提出了一个构造勾股数组的公式,根据该公式可以构造出如下勾股数组:$ (3,4,5),(5,12,13),(7,24,25),… $. 分析上面勾股数组可以发现,$ 4 = 1×(3 + 1),12 = 2×(5 + 1),24 = 3×(7 + 1),… $,利用此规律,第5个勾股数组为(11,60,61).

答案： 5. $(11,60,61)$

6. 若一个三角形的三边之比为$ 5:12:13 $,且周长为60 cm,则它的面积为120cm^{2}.

答案： 6. $120cm^{2}$

1. 如图所示是一块地,已知$ AD = 8m,CD = 6m,∠D = 90^{\circ},AB = 26m,BC = 24m $. 求这块地的面积.

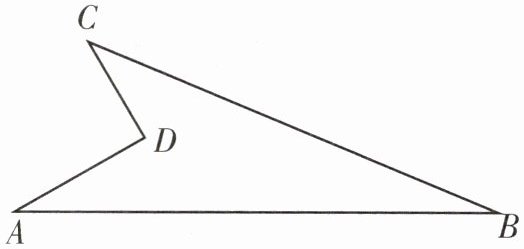
解：连接AC. 在$Rt\triangle ADC$中，$\angle D = 90^{\circ}$，
由勾股定理，得$AC^{2}=AD^{2}+CD^{2}$.
$\because AD = 8$，$CD = 6$，
$\therefore AC^{2}=8^{2}+6^{2}=$100. $\therefore AC = $10.
$\because BC = 24$，$AB = 26$，
$\therefore BC^{2}+AC^{2}=24^{2}+10^{2}=$676，$AB^{2}=26^{2}=$676.
$\therefore BC^{2}+AC^{2}=AB^{2}$.
$\therefore \triangle ABC$是直角三角形，且$\angle ACB = 90^{\circ}$.
$\therefore S_{四边形ADCB}=S_{\triangle ABC}-S_{\triangle ADC}$
$=\frac{1}{2}×24×10-\frac{1}{2}×8×6 = $96$(m^{2})$.
$\therefore$这块地的面积是96$m^{2}$.

答案： 1. 解：连接AC. 在$Rt\triangle ADC$中，$\angle D = 90^{\circ}$，
由勾股定理，得$AC^{2}=AD^{2}+CD^{2}$.
$\because AD = 8$，$CD = 6$，
$\therefore AC^{2}=8^{2}+6^{2}=100$. $\therefore AC = 10$.
$\because BC = 24$，$AB = 26$，
$\therefore BC^{2}+AC^{2}=24^{2}+10^{2}=676$，$AB^{2}=26^{2}=676$.
$\therefore BC^{2}+AC^{2}=AB^{2}$.
$\therefore \triangle ABC$是直角三角形，且$\angle ACB = 90^{\circ}$.
$\therefore S_{四边形ADCB}=S_{\triangle ABC}-S_{\triangle ADC}$
$=\frac{1}{2}×24×10-\frac{1}{2}×8×6 = 96(m^{2})$.
$\therefore$这块地的面积是$96m^{2}$.

2. 我们知道,像3,4,5这样,能够成为直角三角形三条边长的三个正整数,称为勾股数. 古希腊的哲学家柏拉图提出的构造勾股数组的公式为:如果m表示大于1的整数,$ a = 2m,b = m^{2} + 1,c = m^{2} - 1 $,则a,b,c为勾股数.
利用柏拉图公式构造出的勾股数,斜边和其中一直角边的差为2,特别地,当m为大于2的整数时,可以构造出最短边的长度为偶数的勾股数.
任务:(1)请你证明柏拉图公式的正确性.
(2)请你利用柏拉图公式,写出两组勾股数(数据从小到大排列):
第一组:8,15,17;
第二组:12,35,37.

答案： 2.
(1) 证明：$\because m$表示大于1的整数，
$\therefore a$，$b$，$c$都是正整数，且$b$是最大边.
$\because (2m)^{2}+(m^{2}-1)^{2}=(m^{2}+1)^{2}$，
$\therefore a^{2}+c^{2}=b^{2}$.
即$a$，$b$，$c$为勾股数.
(2) 15 17 12 35