《2025年新课堂假期生活暑假生活七年级数学北师大版北京教育出版社》

一、判断题
1. 有两条边对应相等的两个三角形全等. (×)
2. 斜边对应相等的两个等腰直角三角形全等. (√)
3. 有一条直角边对应相等的两个等腰直角三角形全等. (√)
4. 有两个锐角对应相等的两个直角三角形全等. (×)
5. 有一边和一个锐角对应相等的两个直角三角形全等. (√)

答案： 1.× 2.√ 3.√ 4.× 5.√

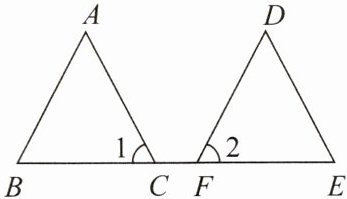
1. 如图,点C,F在BE上,$∠1= ∠2$,$BC= EF$,补充条件$AC = DF$（或$\angle B=\angle E$或$\angle A=\angle D$）,可使$△ABC≌△DEF$.

答案： $AC = DF$（或$\angle B=\angle E$或$\angle A=\angle D$）

2. BD,CE是$△ABC$的两条中线,延长BD到M,使$DM= BD$,延长CE到N,使$EN= CE$,则$∠MAN= $$180^{\circ}$.

答案： $180^{\circ}$

3. 如图,AD,$A'D'$分别是锐角三角形ABC和锐角三角形$A'B'C'$中BC,$B'C'$边上的高,且$AB= A'B'$,$AD= A'D'$,若使$△ABC≌△A'B'C'$,可补充条件：$BC = B'C'$（或$\angle BAC=\angle B'A'C'$或$\angle C=\angle C'$或$DC = D'C'$等）(只填写一个你认为适当的条件).

答案： $BC = B'C'$（或$\angle BAC=\angle B'A'C'$或$\angle C=\angle C'$或$DC = D'C'$等）

4.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的距离DF相等,则∠ABC+∠DFE=90°

答案： 1. 首先，证明$\triangle ABC\cong\triangle DEF$：
在$Rt\triangle ABC$和$Rt\triangle DEF$中，已知$BC = EF$，$AC = DF$。
根据直角 - 斜边 - 直角边（$HL$）定理（若两个直角三角形的斜边和一条直角边分别相等，则这两个直角三角形全等），可得$Rt\triangle ABC\cong Rt\triangle DEF$。
所以$\angle ABC=\angle DEF$。
2. 然后，求$\angle ABC+\angle DFE$的值：
因为在$Rt\triangle DEF$中，$\angle DEF+\angle DFE = 90^{\circ}$（直角三角形两锐角互余，在$Rt\triangle DEF$中，$\angle EDF = 90^{\circ}$，根据三角形内角和定理$\angle DEF+\angle DFE+\angle EDF=180^{\circ}$，即$\angle DEF+\angle DFE=180^{\circ}-\angle EDF$，$\angle EDF = 90^{\circ}$）。
又因为$\angle ABC=\angle DEF$。
所以$\angle ABC+\angle DFE = 90^{\circ}$。
故答案为$90^{\circ}$。

1. 用三角尺可按下面方法画角平分线：在已知$∠AOB的两边上分别取OM= ON$(如图),再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则得到OP平分$∠AOB$. 你知道其中的道理吗？
通过证明$Rt\triangle OMP\cong Rt\triangle ONP$（HL定理），得到对应角$\angle MOP=\angle NOP$，所以$OP$平分$\angle AOB$。

答案： 【解析】：在$Rt\triangle OMP$和$Rt\triangle ONP$中，
因为$OM = ON$（已知），$OP = OP$（公共边），
根据“斜边和一条直角边对应相等的两个直角三角形全等”（HL定理），
所以$Rt\triangle OMP\cong Rt\triangle ONP$。
全等三角形的对应角相等，所以$\angle MOP=\angle NOP$，
即$OP$平分$\angle AOB$。
【答案】：通过证明$Rt\triangle OMP\cong Rt\triangle ONP$（HL定理），得到对应角$\angle MOP=\angle NOP$，所以$OP$平分$\angle AOB$。