《2025年新课堂假期生活暑假生活七年级数学北师大版北京教育出版社》

4. 已知两个三角形的边长分别是 5,5,7；6,6,6. 这两个三角形分别是等腰三角形和等边三角形.

答案： 等腰；等边

5. 如果 $\triangle ABC\cong\triangle DEF$,且 $\triangle ABC$ 的周长为 100 cm,点 A 和 B 的对应点分别为点 D 和 E,已知 $AB = 30\mathrm{cm},DF = 25\mathrm{cm}$,则 $BC=$45cm.

答案： $45\mathrm{cm}$

1. 小颖要制作一个三角形木架,现有长度为 8 m 和 5 m 的木棒各一根. 如果要求第三根木棒的长度是整数,那么小颖有几种选法？第三根木棒的长度可以是多少？

答案： 【解析】：设第三根木棒的长度为$x$米。根据三角形三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，可得$8 - 5\lt x\lt8 + 5$，即$3\lt x\lt13$。因为第三根木棒的长度是整数，所以$x$可以为$4$、$5$、$6$、$7$、$8$、$9$、$10$、$11$、$12$，共$9$种选法。
【答案】：$9$种；$4m$、$5m$、$6m$、$7m$、$8m$、$9m$、$10m$、$11m$、$12m$

2. 甲、乙二人轮流为 $\triangle ABC$(非直角三角形)的 6 个量 $AB,BC,CA,\angle A,\angle B,\angle C$ 赋值,甲先开始. 每次赋值后进行一次判定：若以当前所有已经被赋值的量作为条件,满足条件的 $\triangle ABC$ 多于一种,则游戏继续；否则判最后一个赋值的人失利,另一人获胜. 问：谁有必胜策略？如何取胜？

答案： 甲有必胜策略.

3. 如图,$CD\perp AB$,垂足为点 D,$BE\perp AC$,垂足为点 E,BE,CD 相交于点 O,且 AO 平分 $\angle BAC$. 试问：OB 与 OC 有何大小关系？请说明理由.

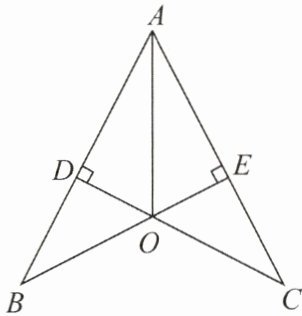
OB 与 OC 的大小关系是OB = OC。理由如下：
因为$AO$平分$\angle BAC$，$CD\perp AB$，$BE\perp AC$，根据角平分线的性质可知角平分线上的点到角两边的距离相等，所以$OD = OE$。
在$\triangle BOD$和$\triangle COE$中，$\angle BDO=\angle CEO = 90^{\circ}$（已知垂直），$\angle BOD=\angle COE$（对顶角相等），$OD = OE$（已证）。
根据“角角边”（$AAS$）全等判定定理，可得$\triangle BOD\cong\triangle COE$。
根据全等三角形的对应边相等，所以$OB = OC$。

答案： 【解析】：
因为$AO$平分$\angle BAC$，$CD\perp AB$，$BE\perp AC$，根据角平分线的性质可知角平分线上的点到角两边的距离相等，所以$OD = OE$。
在$\triangle BOD$和$\triangle COE$中，$\angle BDO=\angle CEO = 90^{\circ}$（已知垂直），$\angle BOD=\angle COE$（对顶角相等），$OD = OE$（已证）。
根据“角角边”（$AAS$）全等判定定理，可得$\triangle BOD\cong\triangle COE$。
根据全等三角形的对应边相等，所以$OB = OC$。
【答案】：$OB = OC$