《2025年新课堂假期生活暑假生活七年级数学北师大版北京教育出版社》

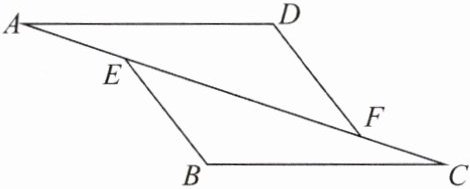
3. 如图,在 $\triangle AFD $ 和 $ \triangle CEB $ 中,点 $ A $,$ E $,$ F $,$ C $ 在同一条直线上,有下面四个论断：
① $ AD = CB $；② $ AE = CF $；③ $ \angle B = \angle D $；④ $ AD // BC $。
请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出解答过程。

已知：在$\triangle AFD$和$\triangle CEB$中，点$A$，$E$，$F$，$C$在同一条直线上，$AE = CF$，$\angle B = \angle D$，$AD // BC$。
求证：$AD = CB$。
证明：因为$AE = CF$，所以$AE + EF = CF + EF$，即$AF = CE$。
因为$AD// BC$，所以$\angle A = \angle C$。
在$\triangle AFD$和$\triangle CEB$中，$\left\{\begin{array}{l}\angle A=\angle C\\\angle D=\angle B\\AF = CE\end{array}\right.$，所以$\triangle AFD\cong\triangle CEB(AAS)$，所以$AD = CB$。

答案： 【解析】：已知在$\triangle AFD$和$\triangle CEB$中，点$A$，$E$，$F$，$C$在同一条直线上，若$AE = CF$，$\angle B=\angle D$，$AD// BC$。
因为$AE = CF$，所以$AE + EF=CF + EF$，即$AF = CE$。
又因为$AD// BC$，所以$\angle A=\angle C$。
在$\triangle AFD$和$\triangle CEB$中，$\left\{\begin{array}{l}\angle A=\angle C\\\angle D=\angle B\\AF = CE\end{array}\right.$，根据$AAS$（两角及其中一角的对边对应相等的两个三角形全等）可得$\triangle AFD\cong\triangle CEB$。
由全等三角形的对应边相等，所以$AD = CB$。
【答案】：以②③④为条件，①为结论。
已知：在$\triangle AFD$和$\triangle CEB$中，点$A$，$E$，$F$，$C$在同一条直线上，$AE = CF$，$\angle B=\angle D$，$AD// BC$。
求证：$AD = CB$。
证明：因为$AE = CF$，所以$AE + EF = CF+EF$，即$AF = CE$。
因为$AD// BC$，所以$\angle A=\angle C$。
在$\triangle AFD$和$\triangle CEB$中，$\left\{\begin{array}{l}\angle A=\angle C\\\angle D=\angle B\\AF = CE\end{array}\right.$，所以$\triangle AFD\cong\triangle CEB(AAS)$，所以$AD = CB$。
（注：也可以以①②④为条件，③为结论等其他组合方式，证明过程类似）