2. 已知 $ \triangle ABC \cong \triangle DEF $,$ \angle A = 53^{\circ} $,$ \angle B = 49^{\circ} $,$ ED = 23 $,则 $ \angle F = $
$78^{\circ}$
,$ AB = $$23$
。
答案:
$78^{\circ}$;$23$
3. 已知 $ \triangle ABC \cong \triangle DEF $,$ A $ 与 $ D $,$ B $ 与 $ E $ 分别是对应顶点,且 $ \angle A = 52^{\circ} $,$ \angle B = 67^{\circ} $,$ BC = 15 \text{ cm} $,则 $ \angle F = $
$61^{\circ}$
,$ FE = $15
$ \text{cm} $。
答案:
$61^{\circ}$,$15$
4. 已知在 $ \triangle ABC $ 和 $ \triangle A'B'C' $ 中,$ AB = A'B' $,$ \angle A = \angle A' $,要使 $ \triangle ABC \cong \triangle A'B'C' $,还需要的条件是
$AC = A'C'$或$\angle B = \angle B'$或$\angle C = \angle C'$
。
答案:
$AC = A'C'$或$\angle B = \angle B'$或$\angle C = \angle C'$
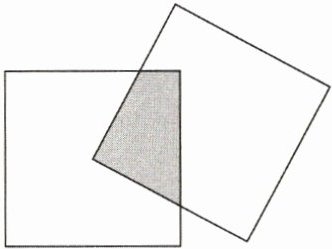
5. 如图,两个同样大的正方形,把其中一个正方形的顶点固定在另一个正方形的中心点上。旋转其中一个正方形,如图所示,重叠部分的面积是 5 平方厘米,则一个正方形的面积是____
20
平方厘米。
答案:
$20$
1. 如图,一个在四个顶点处可挂物品的挂物架,要使其稳定(不变形)地挂在墙上,应如何在顶点处钉钉?为什么?

应

应
在相对的两个顶点之间钉一根钉子
。原因是利用三角形的稳定性,将四边形挂物架分成两个三角形,从而使其稳定不变形
。
答案:
【解析】:根据三角形具有稳定性,四边形具有不稳定性的原理。我们可以在相对的两个顶点之间钉一根钉子,这样就把四边形挂物架分成了两个三角形。因为三角形具有稳定性,所以这样就能使挂物架稳定(不变形)地挂在墙上。
【答案】:在相对的两个顶点之间钉一根钉子。原因是利用三角形的稳定性,将四边形挂物架分成两个三角形,从而使其稳定不变形。
【答案】:在相对的两个顶点之间钉一根钉子。原因是利用三角形的稳定性,将四边形挂物架分成两个三角形,从而使其稳定不变形。
2. 如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ AC = BC $,$ AE $ 是 $ BC $ 边上的中线,过点 $ C $ 作 $ CF \perp AE $,垂足为点 $ F $,过点 $ B $ 作 $ BD \perp BC $ 交 $ CF $ 的延长线于点 $ D $。
(1)试说明 $ AE $ 与 $ CD $ 相等。
解:因为 $ CF \perp AE $,所以 $ \angle CFE = 90^{\circ} $。
因为 $ BD \perp BC $,所以 $ \angle DBC = 90^{\circ} $,
所以 $ \angle D + \angle BCD = 90^{\circ} $,$ \angle AEC + \angle ECF = 90^{\circ} $,又因为 $ \angle BCD = \angle ECF $,所以 $ \angle D = \angle AEC $。
在 $ \triangle DBC $ 和 $ \triangle ECA $ 中,
$ \angle DBC = \angle ECA $,$ BC = AC $,$ \angle D = \angle AEC $,
所以 $ \triangle DBC \cong \triangle ECA $(AAS),
所以 $ AE = CD $。
(2)若 $ AC = 12 \text{ cm} $,求 $ BD $ 的长。
解:由(1)得 $ BD = EC $,又因为 $ BC = AC $,$ AE $ 为 $ BC $ 边上的中线,所以 $ EC = \frac{1}{2}BC = \frac{1}{2}AC $,
所以 $ BD = \frac{1}{2}AC =
(1)试说明 $ AE $ 与 $ CD $ 相等。
解:因为 $ CF \perp AE $,所以 $ \angle CFE = 90^{\circ} $。
因为 $ BD \perp BC $,所以 $ \angle DBC = 90^{\circ} $,
所以 $ \angle D + \angle BCD = 90^{\circ} $,$ \angle AEC + \angle ECF = 90^{\circ} $,又因为 $ \angle BCD = \angle ECF $,所以 $ \angle D = \angle AEC $。
在 $ \triangle DBC $ 和 $ \triangle ECA $ 中,
$ \angle DBC = \angle ECA $,$ BC = AC $,$ \angle D = \angle AEC $,
所以 $ \triangle DBC \cong \triangle ECA $(AAS),
所以 $ AE = CD $。
(2)若 $ AC = 12 \text{ cm} $,求 $ BD $ 的长。
解:由(1)得 $ BD = EC $,又因为 $ BC = AC $,$ AE $ 为 $ BC $ 边上的中线,所以 $ EC = \frac{1}{2}BC = \frac{1}{2}AC $,
所以 $ BD = \frac{1}{2}AC =
6
\text{ cm} $。
答案:
解:
(1) 因为 $ CF \perp AE $,所以 $ \angle DFE = 90^{\circ} $。
因为 $ BD \perp BC $,所以 $ \angle DBC = 90^{\circ} $,
所以 $ \angle D + \angle BEA = 180^{\circ} $。
又因为 $ \angle BEA + \angle AEC = 180^{\circ} $,
所以 $ \angle D = \angle AEC $,$ \angle DCB = \angle EAC $。
在 $ \triangle DBC $ 和 $ \triangle ECA $ 中,
$ \angle DBC = \angle ECA $,$ BC = AC $,$ \angle DCB = \angle EAC $,
所以 $ \triangle DBC \cong \triangle ECA $,
所以 $ AE = CD $。
(2) 由
(1)得 $ BD = EC $,又因为 $ BC = AC $,$ AE $ 为 $ BC $ 边上的中线,所以 $ BC = 2EC = 2BD $,
所以 $ BD = \frac{1}{2}BC = \frac{1}{2}AC = 6 \text{ cm} $。
(1) 因为 $ CF \perp AE $,所以 $ \angle DFE = 90^{\circ} $。
因为 $ BD \perp BC $,所以 $ \angle DBC = 90^{\circ} $,
所以 $ \angle D + \angle BEA = 180^{\circ} $。
又因为 $ \angle BEA + \angle AEC = 180^{\circ} $,
所以 $ \angle D = \angle AEC $,$ \angle DCB = \angle EAC $。
在 $ \triangle DBC $ 和 $ \triangle ECA $ 中,
$ \angle DBC = \angle ECA $,$ BC = AC $,$ \angle DCB = \angle EAC $,
所以 $ \triangle DBC \cong \triangle ECA $,
所以 $ AE = CD $。
(2) 由
(1)得 $ BD = EC $,又因为 $ BC = AC $,$ AE $ 为 $ BC $ 边上的中线,所以 $ BC = 2EC = 2BD $,
所以 $ BD = \frac{1}{2}BC = \frac{1}{2}AC = 6 \text{ cm} $。
查看更多完整答案,请扫码查看


