2. 如图,因为$\triangle ABC \cong \triangle DCB$,所以$\angle A = $
$\angle D$
,$\angle ABC = $$\angle DCB$
,$\angle ACB = $$\angle DBC$
,$AB = $$DC$
,$AC = $$DB$
,$BC = $$CB$
。
答案:
$\angle D$,$\angle DCB$,$\angle DBC$,$DC$,$DB$,$CB$。
3. 如图,$\triangle ADB和\triangle ADC$中,$AB = AC$,$\angle 1 = \angle 2$,加上条件
$AD = AD$(或$\angle B=\angle C$或$\angle ADB=\angle ADC$)
,可得到$\triangle ADB \cong \triangle ADC$,其理由是$SAS$(或$ASA$或$AAS$)
。
答案:
$AD = AD$(或$\angle B=\angle C$或$\angle ADB=\angle ADC$);$SAS$(或$ASA$或$AAS$)
4. 如图,$AE = BE$,$ED = EC$,$\angle C = 90^{\circ}$,$ED \perp AB$,垂足为点$D$,则$\angle A = $

30
$^{\circ}$;若$AB = 6cm$,则$BC = $3
$cm$。
答案:
$30$;$3$
1. 如图,$AE$是一条射线,$\angle BDE = \angle CDE$,$BD = CD$。$AB和AC$相等吗?说明理由。

答:

答:
相等
答案:
相等
2. 如图,$AB = AE$,$\angle B = \angle E$,$BC = ED$,$AF是\angle BAE$的平分线,那么点$F是CD$的中点吗?为什么?
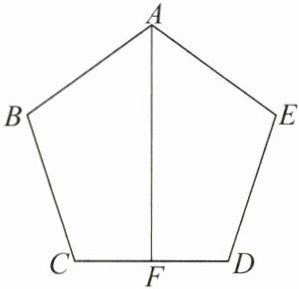
答:

答:
点 F 是 CD 的中点
答案:
点 F 是 CD 的中点.
查看更多完整答案,请扫码查看


