例3 (2025·重庆渝北区期末)如图,小北在公园玩双层型滑梯,每层楼梯的高度相同($BD= DE$),都为2米,他想知道左右两个滑梯$AE和GH$的长度是否相等,于是制定了如下方案:
|课题|探究两个滑梯的长度是否相等|
|测量工具|长度为5米的卷尺|
|测量步骤|①测量出线段$AB$的长度;②测量出线段$IH$的长度|
|测量数据|$IH= 4$米,$AB= 2$米|

(1)根据小明的测量方案和数据,判断两个滑梯$AE和GH$的长度是否相等,并说明理由;
(2)猜想左右两个滑梯$AE和GH$所在直线的位置关系,并加以证明.
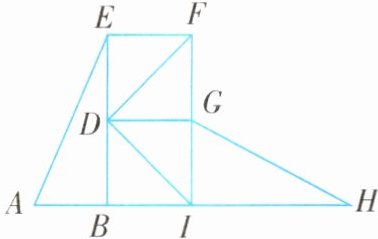
名师启发 (1)由已知条件得出$AB= DB= DE= GI$,$HI= BE$,从而得证$\triangle ABE\cong\triangle GIH$,根据全等三角形的对应边相等得证;
(2)由$\triangle ABE\cong\triangle GIH$,根据全等三角形的对应角相等得$\angle AEB= \angle GHI$,再根据直角三角形两锐角互余,从而得证.
方法技巧
本题考查了全等三角形的判定与性质的应用,把实际问题转化为数学问题是解题的关键.
|课题|探究两个滑梯的长度是否相等|
|测量工具|长度为5米的卷尺|
|测量步骤|①测量出线段$AB$的长度;②测量出线段$IH$的长度|
|测量数据|$IH= 4$米,$AB= 2$米|

(1)根据小明的测量方案和数据,判断两个滑梯$AE和GH$的长度是否相等,并说明理由;
(2)猜想左右两个滑梯$AE和GH$所在直线的位置关系,并加以证明.

名师启发 (1)由已知条件得出$AB= DB= DE= GI$,$HI= BE$,从而得证$\triangle ABE\cong\triangle GIH$,根据全等三角形的对应边相等得证;
(2)由$\triangle ABE\cong\triangle GIH$,根据全等三角形的对应角相等得$\angle AEB= \angle GHI$,再根据直角三角形两锐角互余,从而得证.
方法技巧
本题考查了全等三角形的判定与性质的应用,把实际问题转化为数学问题是解题的关键.
答案:
(1)AE=GH,理由如下:
由题意可知,∠ABE=∠GIH=90°,AB=GI=DB=2米,BE=2×2=4=IH.
在△ABE和△GIH中,AB=GI,∠ABE=∠GIH,BE=IH,
∴△ABE≌△GIH(SAS),
∴AE=GH,即AE和GH的长相等.
(2)AE⊥HG.理由如下:
如图,延长HG交AE于点C.

∵△ABE≌△GIH,
∴∠AEB=∠GHI.
由题意得∠ABE=90°,
∴∠AEB+∠A=90°,
∴∠GHI+∠A=90°,
∴∠ACH=90°,
∴AE⊥GH.
(1)AE=GH,理由如下:
由题意可知,∠ABE=∠GIH=90°,AB=GI=DB=2米,BE=2×2=4=IH.
在△ABE和△GIH中,AB=GI,∠ABE=∠GIH,BE=IH,
∴△ABE≌△GIH(SAS),
∴AE=GH,即AE和GH的长相等.
(2)AE⊥HG.理由如下:
如图,延长HG交AE于点C.

∵△ABE≌△GIH,
∴∠AEB=∠GHI.
由题意得∠ABE=90°,
∴∠AEB+∠A=90°,
∴∠GHI+∠A=90°,
∴∠ACH=90°,
∴AE⊥GH.
例4 (2024·新疆伊犁州期末)如图,在$\triangle ABC$中,$\angle BAC= 60^{\circ}$,$\angle ACB= 40^{\circ}$,点$P$,$Q分别在边BC$,$CA$上,并且$AP$,$BQ分别是\angle BAC$,$\angle ABC$的平分线,请写出$AQ$,$AB$,$BQ$,$BP$之间的数量关系:____.
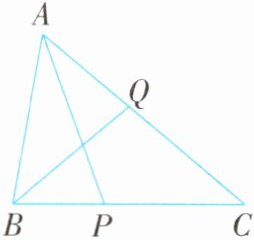
名师启发 延长$AB到点E$,使$BE= BP$,连接$PE$,利用角度关系可求得$BQ= QC$,且可证明$\triangle APE\cong\triangle APC$,得$AE= AC$,即可由$AE= AB+BE= AB+BP$,$AC= AQ+CQ= AQ+BQ$,推导出$AB+BP= AQ+BQ$.

名师启发 延长$AB到点E$,使$BE= BP$,连接$PE$,利用角度关系可求得$BQ= QC$,且可证明$\triangle APE\cong\triangle APC$,得$AE= AC$,即可由$AE= AB+BE= AB+BP$,$AC= AQ+CQ= AQ+BQ$,推导出$AB+BP= AQ+BQ$.
答案:
AB+BP=AQ+BQ [解析]延长AB到点E,使BE=BP,连接PE,则∠E=∠BPE.
∵∠BAC=60°,∠ACB=40°,
∴∠ABC=180°−∠BAC−∠ACB=80°.
∵∠ABC=∠E+∠BPE=2∠E=80°,
∴∠E=40°=∠ACB.
∵AP,BQ分别是∠BAC,∠ABC的平分线,
∴∠BAP=∠CAP,∠QBC=∠ABQ=$\frac{1}{2}$∠ABC =40°=∠ACB,
∴BQ=CQ.
在△APE和△APC中,∠EAP=∠CAP,∠E=∠C,AP=AP,
∴△APE≌△APC(AAS),
∴AE=AC.
∵AE=AB+BE=AB+BP,AC=AQ+CQ=AQ+BQ,
∴AB+BP=AQ+BQ.
∵∠BAC=60°,∠ACB=40°,
∴∠ABC=180°−∠BAC−∠ACB=80°.
∵∠ABC=∠E+∠BPE=2∠E=80°,
∴∠E=40°=∠ACB.
∵AP,BQ分别是∠BAC,∠ABC的平分线,
∴∠BAP=∠CAP,∠QBC=∠ABQ=$\frac{1}{2}$∠ABC =40°=∠ACB,
∴BQ=CQ.
在△APE和△APC中,∠EAP=∠CAP,∠E=∠C,AP=AP,
∴△APE≌△APC(AAS),
∴AE=AC.
∵AE=AB+BE=AB+BP,AC=AQ+CQ=AQ+BQ,
∴AB+BP=AQ+BQ.
查看更多完整答案,请扫码查看


