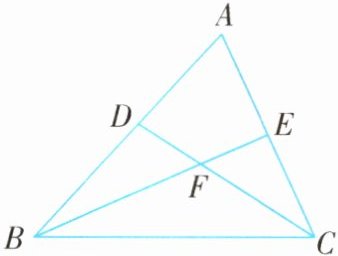
例4 (2025·山东青岛市北区期末)如图,在$\triangle ABC$中,$\angle ABC$,$\angle ACB的平分线BE$,$CD相交于点F$,$\angle A = 58^{\circ}$,则$\angle BFC$的度数为( ).
A.$118^{\circ}$
B.$119^{\circ}$
C.$120^{\circ}$
D.$121^{\circ}$
名师启发 利用三角形的内角和定理及角平分线定义并结合整体思想来进行计算.

A.$118^{\circ}$
B.$119^{\circ}$
C.$120^{\circ}$
D.$121^{\circ}$
名师启发 利用三角形的内角和定理及角平分线定义并结合整体思想来进行计算.
答案:
B [解析]
∵BE平分∠ABC,CD平分∠ACB,
∴∠CBF=$\frac{1}{2}$∠ABC,∠BCF=$\frac{1}{2}$∠ACB,
∴∠CBF+∠BCF=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°−∠A).
∵∠A=58°,
∴∠CBF+∠BCF=$\frac{1}{2}$×(180°−58°)=61°,
∴∠BFC=180°−(∠CBF+∠BCF)=119°.故选B.
∵BE平分∠ABC,CD平分∠ACB,
∴∠CBF=$\frac{1}{2}$∠ABC,∠BCF=$\frac{1}{2}$∠ACB,
∴∠CBF+∠BCF=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°−∠A).
∵∠A=58°,
∴∠CBF+∠BCF=$\frac{1}{2}$×(180°−58°)=61°,
∴∠BFC=180°−(∠CBF+∠BCF)=119°.故选B.
例5 (2025·安徽安庆期中)如图所示,$AD为\triangle ABC$的高,$AE$,$BF为\triangle ABC$的角平分线,若$\angle FBC = 30^{\circ}$,$\angle C = 40^{\circ}$.
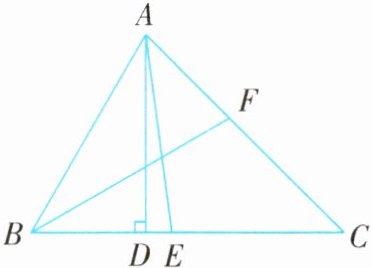
(1)求$\angle DAE$的度数;
(2)若点$M为线段BC$上任意一点,当$\triangle MFC$为直角三角形时,直接写出$\angle BFM$的度数.
名师启发 (1)由角平分线求得$\angle ABC = 60^{\circ}$,由三角形内角和可求得$\angle BAC$,再由角平分线求得$\angle CAE = 40^{\circ}$,由高即可求解;
(2)分两种情况:①当$\angle FMC = 90^{\circ}$时;②当$\angle MFC = 90^{\circ}$时;利用直角三角形性质与三角形外角的性质即可求解.

(1)求$\angle DAE$的度数;
(2)若点$M为线段BC$上任意一点,当$\triangle MFC$为直角三角形时,直接写出$\angle BFM$的度数.
名师启发 (1)由角平分线求得$\angle ABC = 60^{\circ}$,由三角形内角和可求得$\angle BAC$,再由角平分线求得$\angle CAE = 40^{\circ}$,由高即可求解;
(2)分两种情况:①当$\angle FMC = 90^{\circ}$时;②当$\angle MFC = 90^{\circ}$时;利用直角三角形性质与三角形外角的性质即可求解.
答案:
(1)
∵BF平分∠ABC,且∠FBC=30°,
∴∠ABC=2∠FBC=60°,
∴∠BAC=180°−∠ABC−∠C=80°.
∵AE平分∠BAC,
∴∠BAE=∠CAE=$\frac{1}{2}$∠BAC=40°,
∴∠AED=∠CAE+∠C=80°.
∵AD⊥BC,
∴∠DAE=90°−∠AED=10°.
(2)①如图
(1),当∠FMC=90°时,则∠BFM=90°−∠FBC=60°;
②如图
(2),当∠MFC=90°时,则∠FMC=90°−∠C=50°,
∴∠BFM=∠FMC−∠FBC=20°.
综上,∠BFM的度数为20°或60°.
(1)
∵BF平分∠ABC,且∠FBC=30°,
∴∠ABC=2∠FBC=60°,
∴∠BAC=180°−∠ABC−∠C=80°.
∵AE平分∠BAC,
∴∠BAE=∠CAE=$\frac{1}{2}$∠BAC=40°,
∴∠AED=∠CAE+∠C=80°.
∵AD⊥BC,
∴∠DAE=90°−∠AED=10°.
(2)①如图
(1),当∠FMC=90°时,则∠BFM=90°−∠FBC=60°;
②如图
(2),当∠MFC=90°时,则∠FMC=90°−∠C=50°,
∴∠BFM=∠FMC−∠FBC=20°.
综上,∠BFM的度数为20°或60°.
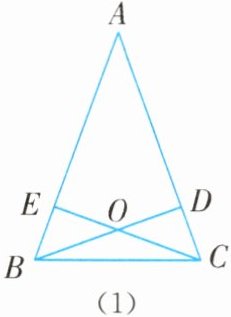
例1 (2025·山东菏泽期中)在$\triangle ABC$中,$\angle A = 40^{\circ}$,高$BD和高CE所在直线交于点O$,则$\angle BOC$的大小为( ).
A.$40^{\circ}或140^{\circ}$
B.$50^{\circ}或130^{\circ}$
C.$40^{\circ}$
D.$50^{\circ}$
解析 根据题意,分两种情况:
当$\triangle ABC$是锐角三角形时,如图(1),
$\because BD和CE$是高,
$\therefore\angle AEO = \angle ADO = 90^{\circ}$,
$\therefore\angle EOD = 360^{\circ} - \angle AEO - \angle ADO - \angle A = 360^{\circ} - 90^{\circ} - 90^{\circ} - 40^{\circ} = 140^{\circ}$,
$\therefore\angle BOC = \angle EOD = 140^{\circ}$;
当$\triangle ABC$是钝角三角形时,如图(2),
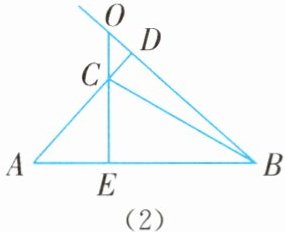
在$\triangle ACE和\triangle OCD$中,$\angle AEC = \angle ODC = 90^{\circ}$,$\angle ACE = \angle OCD$,
$\therefore\angle BOC = \angle A = 40^{\circ}$.
综上所述,$\angle BOC的大小为40^{\circ}或140^{\circ}$.
答案 A

A.$40^{\circ}或140^{\circ}$
B.$50^{\circ}或130^{\circ}$
C.$40^{\circ}$
D.$50^{\circ}$
解析 根据题意,分两种情况:
当$\triangle ABC$是锐角三角形时,如图(1),
$\because BD和CE$是高,
$\therefore\angle AEO = \angle ADO = 90^{\circ}$,
$\therefore\angle EOD = 360^{\circ} - \angle AEO - \angle ADO - \angle A = 360^{\circ} - 90^{\circ} - 90^{\circ} - 40^{\circ} = 140^{\circ}$,
$\therefore\angle BOC = \angle EOD = 140^{\circ}$;
当$\triangle ABC$是钝角三角形时,如图(2),

在$\triangle ACE和\triangle OCD$中,$\angle AEC = \angle ODC = 90^{\circ}$,$\angle ACE = \angle OCD$,
$\therefore\angle BOC = \angle A = 40^{\circ}$.
综上所述,$\angle BOC的大小为40^{\circ}或140^{\circ}$.
答案 A
答案:
A
查看更多完整答案,请扫码查看


