例 1 (2025·上海静安区期中)下列各式计算正确的是( ).
A. $$ a ^ { 3 } + a ^ { 3 } = a ^ { 6 } $B. $$ ( 3 a ) ^ { 3 } = 9 a ^ { 3 } $
C. $$ ( - a ^ { 2 } ) ^ { 2 } = a ^ { 4 } $D. $$ 9 a ^ { 2 } ÷ ( 3 a ^ { 2 } ) = 3 a ^ { 2 } $
解析 A. $$ a ^ { 3 } + a ^ { 3 } = 2 a ^ { 3 } \neq a ^ { 6 } $$,计算错误,不符合题意;
B. $$ ( 3 a ) ^ { 3 } = 3 ^ { 3 } \cdot a ^ { 3 } = 27 a ^ { 3 } \neq 9 a ^ { 3 } $$,计算错误,不符合题意;
C. $$ ( - a ^ { 2 } ) ^ { 2 } = ( - 1 ) ^ { 2 } \cdot a ^ { 2 × 2 } = a ^ { 4 } $$,计算正确,符合题意;
D. $$ 9 a ^ { 2 } ÷ ( 3 a ^ { 2 } ) = 3 \neq 3 a ^ { 2 } $$,计算错误,不符合题意. 故选 C.
A. $$ a ^ { 3 } + a ^ { 3 } = a ^ { 6 } $B. $$ ( 3 a ) ^ { 3 } = 9 a ^ { 3 } $
C. $$ ( - a ^ { 2 } ) ^ { 2 } = a ^ { 4 } $D. $$ 9 a ^ { 2 } ÷ ( 3 a ^ { 2 } ) = 3 a ^ { 2 } $
解析 A. $$ a ^ { 3 } + a ^ { 3 } = 2 a ^ { 3 } \neq a ^ { 6 } $$,计算错误,不符合题意;
B. $$ ( 3 a ) ^ { 3 } = 3 ^ { 3 } \cdot a ^ { 3 } = 27 a ^ { 3 } \neq 9 a ^ { 3 } $$,计算错误,不符合题意;
C. $$ ( - a ^ { 2 } ) ^ { 2 } = ( - 1 ) ^ { 2 } \cdot a ^ { 2 × 2 } = a ^ { 4 } $$,计算正确,符合题意;
D. $$ 9 a ^ { 2 } ÷ ( 3 a ^ { 2 } ) = 3 \neq 3 a ^ { 2 } $$,计算错误,不符合题意. 故选 C.
答案:
【解析】:
本题考查整式的乘法及幂的运算法则。
A项:根据合并同类项,$a^3 + a^3$ 应简化为 $2a^3$,而不是 $a^6$,故A项错误。
B项:根据积的乘方,$(3a)^3$ 应为 $3^3 \cdot a^3 = 27a^3$,而非 $9a^3$,故B项错误。
C项:根据幂的乘方,$(-a^2)^2$ 等于 $(-1)^2 \cdot a^{2 × 2} = a^4$,计算正确,故C项符合题意。
D项:根据单项式除以单项式,$9a^2 ÷ (3a^2)$ 应为 $3$,而非 $3a^2$,故D项错误。
综上所述,正确答案为C。
【答案】:
C
本题考查整式的乘法及幂的运算法则。
A项:根据合并同类项,$a^3 + a^3$ 应简化为 $2a^3$,而不是 $a^6$,故A项错误。
B项:根据积的乘方,$(3a)^3$ 应为 $3^3 \cdot a^3 = 27a^3$,而非 $9a^3$,故B项错误。
C项:根据幂的乘方,$(-a^2)^2$ 等于 $(-1)^2 \cdot a^{2 × 2} = a^4$,计算正确,故C项符合题意。
D项:根据单项式除以单项式,$9a^2 ÷ (3a^2)$ 应为 $3$,而非 $3a^2$,故D项错误。
综上所述,正确答案为C。
【答案】:
C
1. 计算:$$ ( m + n ) ^ { 10 } + ( m + n ) ^ { 10 } = $$____.
答案:
$2(m+n)^{10}$
2. 计算:$$ ( - 3 × 10 ^ { 3 } ) ^ { 3 } = $$____.
答案:
$-2.7×10^{10}$
3. 计算:$$ ( - a ) ^ { 3 } \cdot ( - a ) ^ { 5 } = $$____.
答案:
$a^{8}$
例 2 (2024·江苏扬州邗江区期中)我们学过单项式除以单项式、多项式除以单项式,那么多项式除以多项式该怎么计算呢? 我们也可以用竖式进行类似演算,即先把被除式、除式按某个字母的指数从大到小依次排列项的顺序,并把所缺的次数项用零补齐,再类似数的竖式除法求出商式和余式,其中余式为 0 或余式的次数低于除式的次数.
例:计算 ( 8 x ^ { 2 } + 6 x + 1 ) ÷ ( 2 x + 1 ) ,可依照 672 ÷ 21 的计算方法用竖式进行计算. 因此 ( 8 x ^ { 2 } + 6 x + 1 ) ÷ ( 2 x + 1 ) = 4 x + 1 .
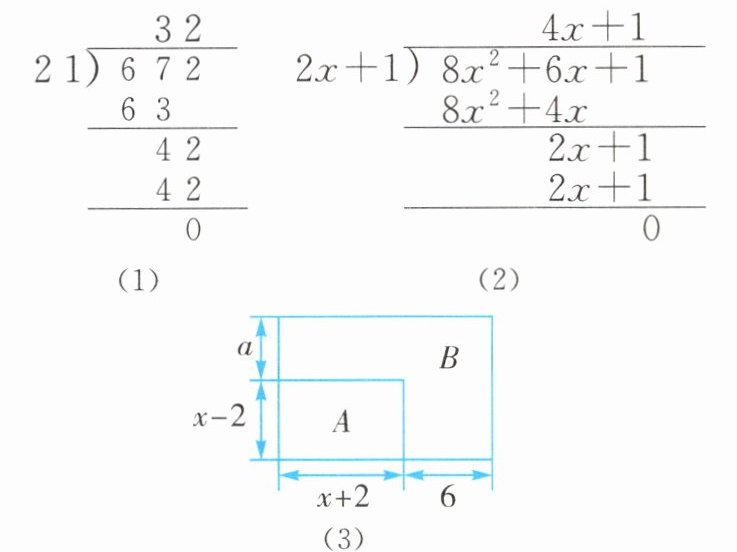
(1) ( 2 x ^ { 2 } + 3 x - 9 ) ÷ ( x + 3 ) = ____.
(2) ( x ^ { 3 } + 4 x ^ { 2 } + 5 x - 6 ) ÷ ( x + 2 ) 的商是____,余式是____.
(3)已知一个长为 ( x + 2 ) ,宽为 ( x - 2 ) 的长方形 A,若将它的长增加 6,宽增加 a 就得到一个新长方形 B,此时长方形 B 的周长是 A 周长的 2 倍(如图(3)). 另有长方形 C 的一边长为 ( x + 10 ) ,若长方形 B 的面积比 C 的面积大 76,求长方形 C 的另一边长(用只含有 x 的代数式表示).
解答 (1) 2 x - 3 提示:用竖式进行计算如下:
$ \begin{array} { r } { 2 x - 3 } \\ { x + 3 \longdiv { 2 x ^ { 2 } + 3 x - 9 } } \\ { \frac { 2 x ^ { 2 } + 6 x } { - 3 x - 9 } } \\ { \frac { - 3 x - 9 } { 0 } } \end{array} $
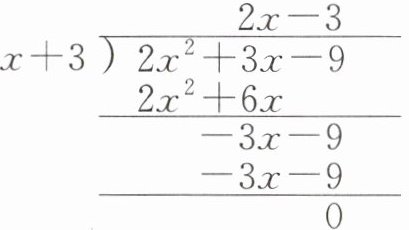
(2) x ^ { 2 } + 2 x + 1 - 8 提示:用竖式进行计算如下:
$ \begin{array} { r } { x ^ { 2 } + 2 x + 1 } \\ { x + 2 \longdiv { x ^ { 3 } + 4 x ^ { 2 } + 5 x - 6 } } \\ { \frac { x ^ { 3 } + 2 x ^ { 2 } } { 2 x ^ { 2 } + 5 x - 6 } } \\ { \frac { 2 x ^ { 2 } + 4 x } { x - 6 } } \\ { \frac { x + 2 } { - 8 } } \end{array} $
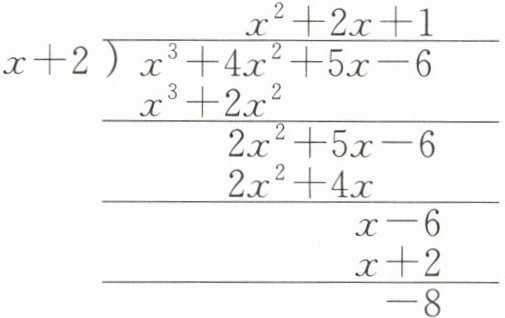
(3)长方形 A 的周长为 2 ( x + 2 + x - 2 ) = 4 x ,长方形 B 的周长为 2 ( x - 2 + a + x + 2 + 6 ) = 4 x + 2 a + 12 .
$ \because $长方形 B 的周长是 A 周长的 2 倍$, \therefore 4 x + 2 a + 12 = 8 x , \therefore a = 2 x - 6 ,$
$ \therefore $长方形 B 的面积为$ ( x + 2 + 6 ) ( x - 2 + 2 x - 6 ) = ( x + 8 ) ( 3 x - 8 ) = 3 x ^ { 2 } + 16 x - 64 , \therefore $长方形 C 的面积为 3 x ^ { 2 } + 16 x - 64 - 76 = 3 x ^ { 2 } + 16 x - 140 ,
$ \therefore $长方形 C 的另一边长为$ ( 3 x ^ { 2 } + 16 x - 140 ) ÷ ( x + 10 ) = 3 x - 14 . \begin{array} { r } { 3 x - 14 } \\ { x + 10 \longdiv { 3 x ^ { 2 } + 16 x - 140 } } \\ { \frac { 3 x ^ { 2 } + 30 x } { - 14 x - 140 } } \\ { \frac { - 14 x - 140 } { 0 } } \end{array} $
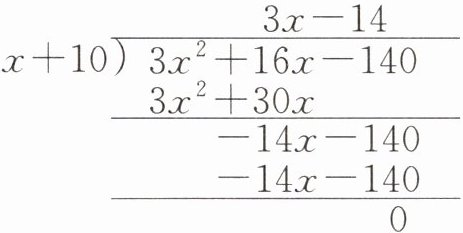
例:计算 ( 8 x ^ { 2 } + 6 x + 1 ) ÷ ( 2 x + 1 ) ,可依照 672 ÷ 21 的计算方法用竖式进行计算. 因此 ( 8 x ^ { 2 } + 6 x + 1 ) ÷ ( 2 x + 1 ) = 4 x + 1 .

(1) ( 2 x ^ { 2 } + 3 x - 9 ) ÷ ( x + 3 ) = ____.
(2) ( x ^ { 3 } + 4 x ^ { 2 } + 5 x - 6 ) ÷ ( x + 2 ) 的商是____,余式是____.
(3)已知一个长为 ( x + 2 ) ,宽为 ( x - 2 ) 的长方形 A,若将它的长增加 6,宽增加 a 就得到一个新长方形 B,此时长方形 B 的周长是 A 周长的 2 倍(如图(3)). 另有长方形 C 的一边长为 ( x + 10 ) ,若长方形 B 的面积比 C 的面积大 76,求长方形 C 的另一边长(用只含有 x 的代数式表示).
解答 (1) 2 x - 3 提示:用竖式进行计算如下:
$ \begin{array} { r } { 2 x - 3 } \\ { x + 3 \longdiv { 2 x ^ { 2 } + 3 x - 9 } } \\ { \frac { 2 x ^ { 2 } + 6 x } { - 3 x - 9 } } \\ { \frac { - 3 x - 9 } { 0 } } \end{array} $
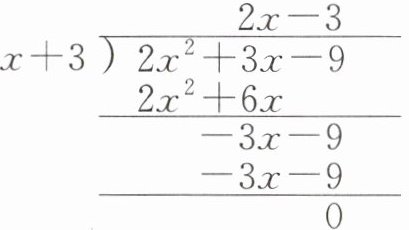
(2) x ^ { 2 } + 2 x + 1 - 8 提示:用竖式进行计算如下:
$ \begin{array} { r } { x ^ { 2 } + 2 x + 1 } \\ { x + 2 \longdiv { x ^ { 3 } + 4 x ^ { 2 } + 5 x - 6 } } \\ { \frac { x ^ { 3 } + 2 x ^ { 2 } } { 2 x ^ { 2 } + 5 x - 6 } } \\ { \frac { 2 x ^ { 2 } + 4 x } { x - 6 } } \\ { \frac { x + 2 } { - 8 } } \end{array} $
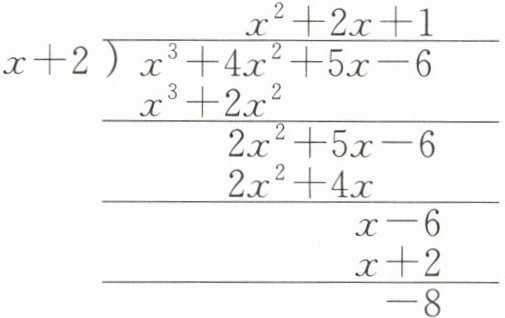
(3)长方形 A 的周长为 2 ( x + 2 + x - 2 ) = 4 x ,长方形 B 的周长为 2 ( x - 2 + a + x + 2 + 6 ) = 4 x + 2 a + 12 .
$ \because $长方形 B 的周长是 A 周长的 2 倍$, \therefore 4 x + 2 a + 12 = 8 x , \therefore a = 2 x - 6 ,$
$ \therefore $长方形 B 的面积为$ ( x + 2 + 6 ) ( x - 2 + 2 x - 6 ) = ( x + 8 ) ( 3 x - 8 ) = 3 x ^ { 2 } + 16 x - 64 , \therefore $长方形 C 的面积为 3 x ^ { 2 } + 16 x - 64 - 76 = 3 x ^ { 2 } + 16 x - 140 ,
$ \therefore $长方形 C 的另一边长为$ ( 3 x ^ { 2 } + 16 x - 140 ) ÷ ( x + 10 ) = 3 x - 14 . \begin{array} { r } { 3 x - 14 } \\ { x + 10 \longdiv { 3 x ^ { 2 } + 16 x - 140 } } \\ { \frac { 3 x ^ { 2 } + 30 x } { - 14 x - 140 } } \\ { \frac { - 14 x - 140 } { 0 } } \end{array} $
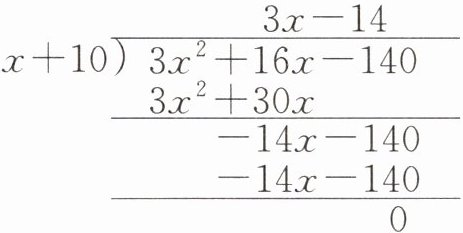
答案:
(1) $2x - 3$
(2) $x^2 + 2x + 1$;$-8$
(3) 解:长方形 A 的周长为 $2[(x + 2) + (x - 2)] = 4x$。
长方形 B 的长为 $x + 2 + 6 = x + 8$,宽为 $x - 2 + a$,周长为 $2[(x + 8) + (x - 2 + a)] = 4x + 2a + 12$。
由题意得 $4x + 2a + 12 = 2 × 4x$,解得 $a = 2x - 6$。
长方形 B 的宽为 $x - 2 + 2x - 6 = 3x - 8$,面积为 $(x + 8)(3x - 8) = 3x^2 + 16x - 64$。
长方形 C 的面积为 $3x^2 + 16x - 64 - 76 = 3x^2 + 16x - 140$。
另一边长为 $(3x^2 + 16x - 140) ÷ (x + 10) = 3x - 14$。
答:长方形 C 的另一边长为 $3x - 14$。
(1) $2x - 3$
(2) $x^2 + 2x + 1$;$-8$
(3) 解:长方形 A 的周长为 $2[(x + 2) + (x - 2)] = 4x$。
长方形 B 的长为 $x + 2 + 6 = x + 8$,宽为 $x - 2 + a$,周长为 $2[(x + 8) + (x - 2 + a)] = 4x + 2a + 12$。
由题意得 $4x + 2a + 12 = 2 × 4x$,解得 $a = 2x - 6$。
长方形 B 的宽为 $x - 2 + 2x - 6 = 3x - 8$,面积为 $(x + 8)(3x - 8) = 3x^2 + 16x - 64$。
长方形 C 的面积为 $3x^2 + 16x - 64 - 76 = 3x^2 + 16x - 140$。
另一边长为 $(3x^2 + 16x - 140) ÷ (x + 10) = 3x - 14$。
答:长方形 C 的另一边长为 $3x - 14$。
查看更多完整答案,请扫码查看


