《2025年实验班提优训练八年级数学上册人教版》

7. (2025·福建厦门思明区期末)在直角三角形中,过一个锐角顶点的一条直线将直角三角形分成一个直角三角形和一个等腰三角形,则称这条直线是该直角三角形的“直角等腰线”。
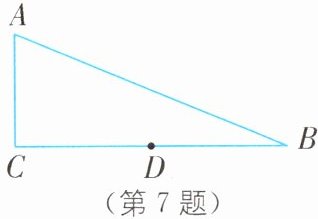
(1)如图,在Rt△ABC中,∠C = 90°,∠B = 22.5°,若∠CAD = 2∠BAD,判断AD是否为Rt△ABC的“直角等腰线”,并说明理由；
(2)在Rt△ABC中,∠C = 90°,∠BAC = 60°,BC = 6。若AD为Rt△ABC的“直角等腰线”,求点D到AB的距离。

答案：

(1)AD是Rt△ABC的“直角等腰线”，理由如下：在Rt△ABC中，∠C=90°,∠B=22.5°,
∴∠CAB=67.5°.
∵∠CAD=2∠BAD,
∴∠DAB=$\frac{1}{3}$×67.5°=22.5°,
∴∠DAB=∠B,
∴△ADB是等腰三角形，△ACD是直角三角形，
∴AD是Rt△ABC的“直角等腰线”.
(2)
∵在Rt△ABC中，∠C=90°,∠BAC=60°,BC=6,
∴∠B=30°.
∵AD为Rt△ABC的“直角等腰线”，
∴∠DAB=30°,∠CAD=60°−30°=30°.
　　　　　　
过点D作DE⊥AB，垂足为E.
∵∠CAD=∠DAB=30°,
∴CD=DE.
∵BC=CD+BD=DE+BD=6,∠B=30°,
∴DE=$\frac{1}{2}BD=\frac{1}{3}BC=\frac{1}{3}×6 = 2$，
∴点D到AB的距离为2.

8. 如图(1),点P,Q分别是等边三角形ABC边AB,BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的运动速度相同,连接AQ,CP交于点M。
(1)求证：△ABQ≌△CAP。
(2)当点P,Q分别在AB,BC边上运动时,∠QMC变化吗？若变化,请说明理由；若不变,求出它的度数。
(3)如图(2),若点P,Q在运动到终点后继续在射线AB,BC上运动,直线AQ,CP交点为M,则∠QMC变化吗？若变化,请说明理由；若不变,则求出它的度数。

答案：
(1)
∵△ABC是等边三角形，
∴∠ABQ=∠CAP,AB=CA.又点P，Q运动速度相同，
∴AP=BQ.在△ABQ与△CAP中，$\begin{cases}AB = CA\\∠ABQ = ∠CAP\\AP = BQ\end{cases}$
∴△ABQ≌△CAP(SAS).
(2)点P,Q在运动的过程中，∠QMC不变，理由如下：
∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC=∠ACP+∠MAC,
∴∠QMC=∠BAQ+∠MAC=∠BAC=60°.
(3)点P，Q在运动到终点后继续在射线AB、BC上运动时，∠QMC不变化.理由如下：
∵△ABQ≌△CAP,
∴∠BAQ=∠ACP.
∵∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°−∠PAC=180°−60°=120°.