例1 (2024·黑龙江牡丹江宁安期末)作图题:(不写作法,但必须保留作图痕迹)
如图,某地有两所大学和两条相交叉的公路(点M,N表示大学,AO,BO表示公路)。现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等。你能确定仓库P应该建在什么位置吗?在所给的图形中画出你的设计方案。
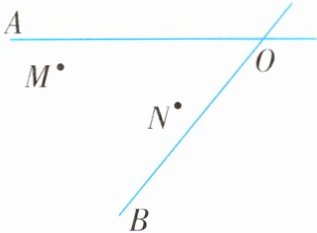
解答 如图所示:

(1)连接MN,分别以M,N为圆心,以大于$\frac{1}{2}$MN的长为半径画弧,两弧相交于D,E,连接DE,则DE即为线段MN的垂直平分线;(2)以O为圆心,以任意长为半径画弧,分别交OA,OB于G,H,再分别以G,H为圆心,以大于$\frac{1}{2}$GH的长为半径画弧,两弧相交于F,连接OF,则OF即为∠AOB的平分线(或∠AOB的外角平分线);(3)DE与OF相交于点P,则点P即为所求。
如图,某地有两所大学和两条相交叉的公路(点M,N表示大学,AO,BO表示公路)。现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等。你能确定仓库P应该建在什么位置吗?在所给的图形中画出你的设计方案。

解答 如图所示:

(1)连接MN,分别以M,N为圆心,以大于$\frac{1}{2}$MN的长为半径画弧,两弧相交于D,E,连接DE,则DE即为线段MN的垂直平分线;(2)以O为圆心,以任意长为半径画弧,分别交OA,OB于G,H,再分别以G,H为圆心,以大于$\frac{1}{2}$GH的长为半径画弧,两弧相交于F,连接OF,则OF即为∠AOB的平分线(或∠AOB的外角平分线);(3)DE与OF相交于点P,则点P即为所求。
答案:
【解析】:
本题主要考查线段的垂直平分线和角平分线的作法,以及这两条线的性质。
(1) 线段的垂直平分线上的点到线段两端点的距离相等。所以要使仓库到两所大学的距离相等,需作线段$MN$的垂直平分线。
(2) 角平分线上的点到角两边的距离相等。所以要使仓库到两条公路的距离相等,需作$\angle AOB$的平分线(或$\angle AOB$的外角平分线)。
(3) 线段$MN$的垂直平分线与$\angle AOB$的平分线(或$\angle AOB$的外角平分线)的交点,即为满足仓库到两所大学距离相等且到两条公路距离也相等的位置。
【答案】:
(1) 连接$MN$,分别以$M$,$N$为圆心,以大于$\frac{1}{2}MN$的长为半径画弧,两弧相交于$D$,$E$,连接$DE$,则$DE$即为线段$MN$的垂直平分线;
(2) 以$O$为圆心,以任意长为半径画弧,分别交$OA$,$OB$于$G$,$H$,再分别以$G$,$H$为圆心,以大于$\frac{1}{2}GH$的长为半径画弧,两弧相交于$F$,连接$OF$,则$OF$即为$\angle AOB$的平分线(或$\angle AOB$的外角平分线);
(3) $DE$与$OF$相交于点$P$,则点$P$即为所求。
本题主要考查线段的垂直平分线和角平分线的作法,以及这两条线的性质。
(1) 线段的垂直平分线上的点到线段两端点的距离相等。所以要使仓库到两所大学的距离相等,需作线段$MN$的垂直平分线。
(2) 角平分线上的点到角两边的距离相等。所以要使仓库到两条公路的距离相等,需作$\angle AOB$的平分线(或$\angle AOB$的外角平分线)。
(3) 线段$MN$的垂直平分线与$\angle AOB$的平分线(或$\angle AOB$的外角平分线)的交点,即为满足仓库到两所大学距离相等且到两条公路距离也相等的位置。
【答案】:
(1) 连接$MN$,分别以$M$,$N$为圆心,以大于$\frac{1}{2}MN$的长为半径画弧,两弧相交于$D$,$E$,连接$DE$,则$DE$即为线段$MN$的垂直平分线;
(2) 以$O$为圆心,以任意长为半径画弧,分别交$OA$,$OB$于$G$,$H$,再分别以$G$,$H$为圆心,以大于$\frac{1}{2}GH$的长为半径画弧,两弧相交于$F$,连接$OF$,则$OF$即为$\angle AOB$的平分线(或$\angle AOB$的外角平分线);
(3) $DE$与$OF$相交于点$P$,则点$P$即为所求。
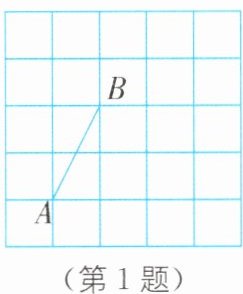
1. 在如图所示的方格纸中,每个小正方形的边长均为1.点A,B是方格纸中的两个格点(正方形的顶点),在这个5×5的方格纸中,若△ABC是等腰三角形,则满足条件的格点C有( )。
A.6个
B.7个
C.8个
D.9个

A.6个
B.7个
C.8个
D.9个
答案:
D [解析]如图所示,以A为顶角顶点的等腰三角形共3个(包括线段AB的垂直平分线的情况),以B为顶角顶点的等腰三角形共有6个,所以满足条件的格点C有9个.故选D.

易错警示:本题需要考虑以AB为底和以AB为腰,以AB为腰又要考虑以A为顶点和以B为顶点,如果考虑不全面就会错解或漏解.
D [解析]如图所示,以A为顶角顶点的等腰三角形共3个(包括线段AB的垂直平分线的情况),以B为顶角顶点的等腰三角形共有6个,所以满足条件的格点C有9个.故选D.

易错警示:本题需要考虑以AB为底和以AB为腰,以AB为腰又要考虑以A为顶点和以B为顶点,如果考虑不全面就会错解或漏解.
2. (2025·安徽淮南期末)如图,平面直角坐标系中,点A,B分别在y轴和x轴上,∠ABO = 60°,在坐标轴上找一点P,使得△PAB是等腰三角形,则符合条件的P点共有( )个。

A.8
B.7
C.6
D.5

A.8
B.7
C.6
D.5
答案:
C [解析]①当AB=AP时,在y轴上有2个满足条件的点P,在x轴上有1个满足条件的点P;②当AB=BP时,在y轴上有1个满足条件的点P,在x轴上有2个满足条件的点P,有1点与AB=AP时的x轴正半轴的点P重合;③当AP=BP时,在x轴、y轴上各有1个满足条件的点P,有1点与AB=AP时的x轴正半轴的点P重合.综上所述,符合条件的点P共有6个.故选C.
3. (2025·湖北荆门期末)定义:等腰三角形的底边长与其腰长的比值k称为这个等腰三角形的“优美比”。若等腰三角形的周长为13 cm,AB = 5 cm,则它的“优美比”k为( )。
A.$\frac{5}{4}$
B.$\frac{3}{5}$
C.$\frac{5}{4}或\frac{3}{5}$
D.$\frac{4}{5}或\frac{5}{3}$
A.$\frac{5}{4}$
B.$\frac{3}{5}$
C.$\frac{5}{4}或\frac{3}{5}$
D.$\frac{4}{5}或\frac{5}{3}$
答案:
C [解析]分两种情况:当等腰三角形的腰长为5cm时,
∵等腰三角形的周长为13cm,
∴等腰三角形的底边长=13−5−5=3(cm),
∴这个等腰三角形的“优美比”=$\frac{3}{5}$;当等腰三角形的底边长为5cm时,
∵等腰三角形的周长为13cm,
∴等腰三角形的腰长=$\frac{13 - 5}{2}$=4(cm),
∴这个等腰三角形的“优美比”=$\frac{5}{4}$.综上所述,它的“优美比”k为$\frac{3}{5}$或$\frac{5}{4}$.故选C.
∵等腰三角形的周长为13cm,
∴等腰三角形的底边长=13−5−5=3(cm),
∴这个等腰三角形的“优美比”=$\frac{3}{5}$;当等腰三角形的底边长为5cm时,
∵等腰三角形的周长为13cm,
∴等腰三角形的腰长=$\frac{13 - 5}{2}$=4(cm),
∴这个等腰三角形的“优美比”=$\frac{5}{4}$.综上所述,它的“优美比”k为$\frac{3}{5}$或$\frac{5}{4}$.故选C.
4. 如图,平面直角坐标系中存在点A(3,2),点B(1,0),以线段AB为边作等腰三角形ABP,使得点P在坐标轴上,则这样的点P有( )。

A.4个
B.5个
C.7个
D.8个

A.4个
B.5个
C.7个
D.8个
答案:
C [解析]如图,

以A为圆心,AB长为半径画圆,与x轴有1个交点(除点B以外);以B为圆心,AB长为半径画圆,与x轴有2个交点,与y轴有2个交点;作AB的垂直平分线,与x轴、y轴各有1个交点,
∴这样的点P有7个.故选C.
思路引导:按照上面几题的经验应该有8个点满足条件,但通过作图发现以点A为圆心,BA长为半径的圆与y轴没有交点,故本题只有7个点满足条件.
C [解析]如图,

以A为圆心,AB长为半径画圆,与x轴有1个交点(除点B以外);以B为圆心,AB长为半径画圆,与x轴有2个交点,与y轴有2个交点;作AB的垂直平分线,与x轴、y轴各有1个交点,
∴这样的点P有7个.故选C.
思路引导:按照上面几题的经验应该有8个点满足条件,但通过作图发现以点A为圆心,BA长为半径的圆与y轴没有交点,故本题只有7个点满足条件.
查看更多完整答案,请扫码查看


