3.如图(1),在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,点$D在边BC$上,点$E在边AD$上,$AD= BD$,$\angle ABE= \angle CAD+\angle CBE$.
(1)求证:$\angle BAC= 2\angle ABE$;
(2)作$EF\perp AB$,垂足为$F$(如图(2)),探究线段$CD$,$DE$,$EF$之间的数量关系并证明.
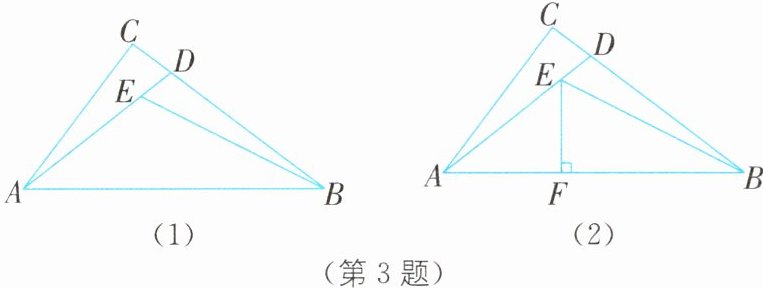
(1)求证:$\angle BAC= 2\angle ABE$;
(2)作$EF\perp AB$,垂足为$F$(如图(2)),探究线段$CD$,$DE$,$EF$之间的数量关系并证明.

答案:
(1)
∵AD=BD,
∴∠DAB=∠DBA=∠CBE+∠ABE.
∴∠BAC=∠CAD+∠DAB=∠CAD+∠CBE+∠ABE.
∵∠ABE=∠CAD+∠CBE,
∴∠BAC=2∠ABE.
(2)EF=CD+DE.理由如下:
如图,过点B作BG⊥AD,交AD的延长线于点G.

在△ACD和△BGD中,∠C=∠G=90°,∠ADC=∠BDG,AD=BD,
∴△ACD≌△BGD(AAS).
∴CD=DG,∠CAD=∠GBD.
∵∠GBE=∠GBD+∠CBE,∠ABE=∠CAD+∠CBE,
∴∠GBE=∠ABE.
又EF⊥AB,EG⊥GB,
∴△BEF≌△BEG,
∴EF=EG.
∵EG=DG+DE=CD+DE,
∴EF=CD+DE.
归纳总结:解答本题需要利用全等三角形的判定和性质,过点B作BG⊥AD,交AD的延长线于点G,构造全等三角形是解答本题的关键.
(1)
∵AD=BD,
∴∠DAB=∠DBA=∠CBE+∠ABE.
∴∠BAC=∠CAD+∠DAB=∠CAD+∠CBE+∠ABE.
∵∠ABE=∠CAD+∠CBE,
∴∠BAC=2∠ABE.
(2)EF=CD+DE.理由如下:
如图,过点B作BG⊥AD,交AD的延长线于点G.

在△ACD和△BGD中,∠C=∠G=90°,∠ADC=∠BDG,AD=BD,
∴△ACD≌△BGD(AAS).
∴CD=DG,∠CAD=∠GBD.
∵∠GBE=∠GBD+∠CBE,∠ABE=∠CAD+∠CBE,
∴∠GBE=∠ABE.
又EF⊥AB,EG⊥GB,
∴△BEF≌△BEG,
∴EF=EG.
∵EG=DG+DE=CD+DE,
∴EF=CD+DE.
归纳总结:解答本题需要利用全等三角形的判定和性质,过点B作BG⊥AD,交AD的延长线于点G,构造全等三角形是解答本题的关键.
4.(2025·吉林四平铁东区期末)如图所示,在长方形$ABCD$中,$AB= 4cm$,$AD= 8cm$.点$P从点A$出发,沿边$AD由A—D—A$做往返运动,每秒移动$2cm$,动直线$a与边CD$重合,交$AD于点M$,$BC于点N$.直线$a与点P$同时出发,沿$DA$方向移动,每秒移动$1cm$,移动$t$秒($t>0$),当直线$a与边AB$重合时,移动全部停止.
(1)用含$t的代数式表示AP$的长度;
(2)当$t$为何值时,点$P在直线a$上;
(3)连接$PB$,$PN$,直接写出当$t$为何值时,$\triangle PAB与\triangle PMN$全等.
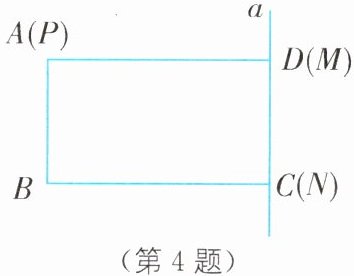
(1)用含$t的代数式表示AP$的长度;
(2)当$t$为何值时,点$P在直线a$上;
(3)连接$PB$,$PN$,直接写出当$t$为何值时,$\triangle PAB与\triangle PMN$全等.

答案:
(1)当直线a运动到AB时,t=8÷1=8(秒),
∴当t=8时,移动全部停止,
∴当0<t≤4时,AP=2t;
当4<t≤8时,AP=16−2t,
综上,AP={2t(0<t≤4),16−2t(4<t≤8)}.
(2)直线a与AB的距离为8−t.
当点P在直线a上时,8−t=2t或8−t=16−2t,解得t=$\frac{8}{3}$或8.
∴当t为$\frac{8}{3}$或8时,点P在直线a上.
(3)①当Rt△PAB≌Rt△PMN时,PA=PM,AB=MN,
∵PA=2t,DM=t,
∴PM=8−3t,
∴2t=8−3t,解得t=$\frac{8}{5}$
②当Rt△PAB≌Rt△NMP时,PA=MN,且AB=PM,即2t=4,且4=8−3t (需要同时满足),
∴t=2且t=$\frac{4}{3}$,
∴这种情况不成立.
综上,当t=$\frac{8}{5}$时,△PAB与△PMN全等.

(1)当直线a运动到AB时,t=8÷1=8(秒),
∴当t=8时,移动全部停止,
∴当0<t≤4时,AP=2t;
当4<t≤8时,AP=16−2t,
综上,AP={2t(0<t≤4),16−2t(4<t≤8)}.
(2)直线a与AB的距离为8−t.
当点P在直线a上时,8−t=2t或8−t=16−2t,解得t=$\frac{8}{3}$或8.
∴当t为$\frac{8}{3}$或8时,点P在直线a上.
(3)①当Rt△PAB≌Rt△PMN时,PA=PM,AB=MN,
∵PA=2t,DM=t,
∴PM=8−3t,
∴2t=8−3t,解得t=$\frac{8}{5}$
②当Rt△PAB≌Rt△NMP时,PA=MN,且AB=PM,即2t=4,且4=8−3t (需要同时满足),
∴t=2且t=$\frac{4}{3}$,
∴这种情况不成立.
综上,当t=$\frac{8}{5}$时,△PAB与△PMN全等.

查看更多完整答案,请扫码查看


