2. (2025·广东东莞期末)我国数学家华罗庚曾用诗词表达了“数形结合”的思想,其中谈到“数缺形时少直观,形少数时难入微. 数形结合百般好,隔离分家万事休.”请利用“数形结合”的思想解决以下问题.
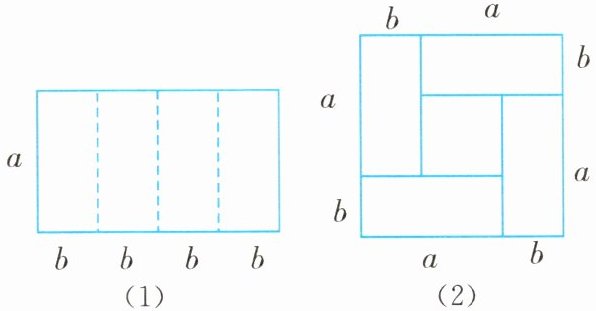
图(1)是一个长为 4b,宽为$$ a ( a > b ) $$的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按如图(2)所示的形状拼得一个大正方形.
(1)观察图(1),图(2),请写出$$ ( a + b ) ^ { 2 } $$,$$ ( a - b ) ^ { 2 } $$,ab 之间的等量关系:____;
(2)如图(3),正方形 ABCD 的边长为 a,正方形 CEFG 的边长 b,点 E,G 分别在 CD,BC 边上. 若$$ a + b = 13 $$,$$ a b = 32 $$,求图中阴影部分的面积.

图(1)是一个长为 4b,宽为$$ a ( a > b ) $$的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按如图(2)所示的形状拼得一个大正方形.
(1)观察图(1),图(2),请写出$$ ( a + b ) ^ { 2 } $$,$$ ( a - b ) ^ { 2 } $$,ab 之间的等量关系:____;
(2)如图(3),正方形 ABCD 的边长为 a,正方形 CEFG 的边长 b,点 E,G 分别在 CD,BC 边上. 若$$ a + b = 13 $$,$$ a b = 32 $$,求图中阴影部分的面积.


答案:
(1)$(a+b)^{2}=(a-b)^{2}+4ab$
(2)$S_{阴影部分}=\frac{1}{2}a(a-b)+\frac{1}{2}b^{2}=\frac{1}{2}(a^{2}-ab+b^{2})=\frac{1}{2}[(a+b)^{2}-3ab]=\frac{1}{2}×(13^{2}-3×32)=\frac{73}{2}$.
(1)$(a+b)^{2}=(a-b)^{2}+4ab$
(2)$S_{阴影部分}=\frac{1}{2}a(a-b)+\frac{1}{2}b^{2}=\frac{1}{2}(a^{2}-ab+b^{2})=\frac{1}{2}[(a+b)^{2}-3ab]=\frac{1}{2}×(13^{2}-3×32)=\frac{73}{2}$.
查看更多完整答案,请扫码查看


