《2025年实验班提优训练八年级数学上册人教版》

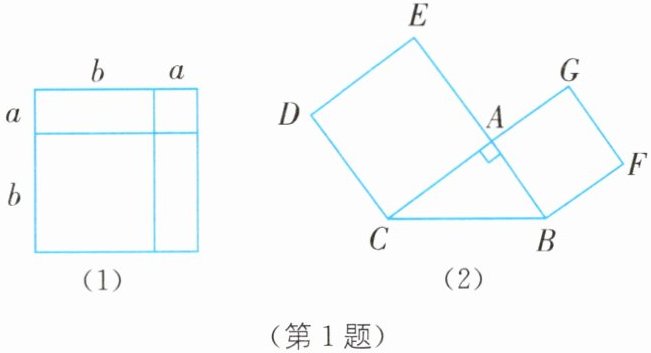
1. (2025·广东广州花都区期末)基本知识：通过用两种不同方法计算图(1)的面积,发现：$$ ( a + b ) ^ { 2 } = a ^ { 2 } + 2 a b + b ^ { 2 } $$恒成立. 基于此,请解答下列问题：
(1)直接应用：若$$ a b = 4 $$,$$ a + b = 5 $$,直接写出$$ a ^ { 2 } + b ^ { 2 } $$的值为____；
(2)类比应用：若$$ a ( 3 - a ) = 2 $$,则$$ a ^ { 2 } + ( 3 - a ) ^ { 2 } = $$____；
(3)拓展迁移：为落实国家劳动实践教育的政策,使同学们体验劳动的快乐,掌握劳动技能,某学校计划组织八年级的学生在学校实践园开展劳动实践活动. 首先在实践园用栅栏围成一个$$ \triangle A B C $$区域,用来种植草坪(如图(2)),其中$$ A C \perp A B $$于点 A,AC 与 AB 两边的长度和为 30 m,然后再以 AC,AB 为边分别向外扩建成正方形 ACDE 和正方形 ABFG 的用地,分别种植三角梅和月季花,向外扩建的两个正方形面积和为$$ 500 \text { m } ^ { 2 } $$. 请根据题意求种植草坪的$$ \triangle A B C $$的面积.

答案：
(1)17 [解析]$\because (a+b)^{2}=a^{2}+2ab+b^{2},ab=4,a+b=5$，$\therefore 5^{2}=a^{2}+2×4+b^{2},\therefore a^{2}+b^{2}=17$.
(2)5 [解析]设$x=a,y=3-a$，则$xy=a(3-a)=2,x+y=3$，所以$a^{2}+(3-a)^{2}=x^{2}+y^{2}=(x+y)^{2}-2xy=9-4=5$.
(3)设$AC=a,AB=b$，由题意，得$a+b=AC+AB=30\ m,a^{2}+b^{2}=500\ m^{2}$，$\therefore S_{\triangle ABC}=\frac{1}{2}AC\cdot AB=\frac{1}{2}ab=\frac{1}{2}×\frac{1}{2}[(a+b)^{2}-(a^{2}+b^{2})]=\frac{1}{4}×(900-500)=100(m^{2})$.

例 2 (2025·湖北鄂州期末)[知识生成]通过本章的学习,我们已经知道,对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式,请结合图形解答下列问题：

(1)图(1)中所表示的数学等式是____；
(2)如图(2),是用 4 块完全相同的长方形拼成的正方形,用两种不同的方法求图中阴影部分的面积,得到的数学等式是____；
[知识应用](3)若$ x + y = 7 , x y = \frac { 13 } { 4 } ,$求 x - y 的值；
[灵活应用](4)图(3)中有两个正方形 A,B,现将 B 放在 A 的内部得到图甲,将 A,B 并列放置后构造新的正方形得到图乙. 若图甲和图乙中阴影部分的面积分别为 2 和 11,则正方形 A,B 的面积之和为____.
解析 (1)根据大正方形面积 = 两个边长分别为 a,b 的小正方形面积 + 2 个长方形面积进行求解即可；(2)根据空白部分的面积 = 大正方形面积 - 4 个长方形面积进行求解即可；(3)根据(2)中得到的等式即可求解；(4)根据图甲和图乙的阴影部分面积求出 ( a - b ) ^ { 2 } = 2 , 2 a b = 11 ,据此求解即可.
答案 (1) ( a + b ) ^ { 2 } = a ^ { 2 } + 2 a b + b ^ { 2 } (2) ( a + b ) ^ { 2 } - ( a - b ) ^ { 2 } = 4 a b
$(3) \because x + y = 7 , \therefore ( x + y ) ^ { 2 } = 49 ,$
$ \therefore ( x - y ) ^ { 2 } = ( x + y ) ^ { 2 } - 4 x y = 49 - 4 × \frac { 13 } { 4 } = 36 , \therefore x - y = \pm 6 .(4)13$点拨完全平方公式的两个变形拓展公式：(1) a ^ { 2 } + b ^ { 2 } = ( a - b ) ^ { 2 } + 2 a b ；(2) ( a + b ) ^ { 2 } - ( a - b ) ^ { 2 } = 4 a b .

答案： 【解析】：
(1)观察图
(1)，可以得到：
大正方形的边长为$a+b$，根据正方形面积公式，其面积为$(a+b)^{2}$。
同时，大正方形内部包含两个边长分别为$a$和$b$的小正方形，以及两个长方形，小正方形面积分别为$a^{2}$和$b^{2}$，两个长方形面积均为$ab$，所以图形总面积还可以表示为$a^{2}+2ab+b^{2}$。
因此，图
(1)所表示的数学等式是$(a+b)^{2}=a^{2}+2ab+b^{2}$。
(2)对于图
(2)，求阴影部分的面积有两种方法：
方法一：大正方形的边长为$a+b$，其面积为$(a+b)^{2}$。
方法二：阴影部分是由四个长方形围成的中间空的正方形，空白正方形的边长为$a-b$，其面积为$(a-b)^{2}$，而四个长方形面积总和为$4ab$，所以阴影部分面积还可以表示为$(a+b)^{2}-4ab$。
由此可得数学等式$(a+b)^{2}-(a-b)^{2}=4ab$。
(3)已知$x+y=7$，对等式两边同时平方可得$(x+y)^{2}=49$。
根据完全平方公式$(x+y)^{2}=x^{2}+2xy+y^{2}$，$(x-y)^{2}=x^{2}-2xy+y^{2}$，可以推导出$(x-y)^{2}=(x+y)^{2}-4xy$。
将$x+y=7$，$xy=\frac{13}{4}$代入上式，可得$(x-y)^{2}=49-4×\frac{13}{4}=36$，所以$x-y=\pm6$。
(4)设正方形A的边长为$a$，正方形B的边长为$b$。
对于图甲，阴影部分面积等于大正方形面积减去小正方形面积，即$(a-b)^{2}=2$。
对于图乙，阴影部分面积可以看作是边长为$a+b$的正方形面积减去两个正方形A和B的面积后剩余的部分，其面积为$2ab=11$。
根据完全平方公式$a^{2}+b^{2}=(a-b)^{2}+2ab$，将$(a-b)^{2}=2$，$2ab=11$代入可得：
$a^{2}+b^{2}=2+11=13$，即三个正方形A，B的面积之和为13。
【答案】：
(1)$(a+b)^{2}=a^{2}+2ab+b^{2}$；
(2)$(a+b)^{2}-(a-b)^{2}=4ab$；
(3)$x-y=\pm6$；
(4)13。