《2025年实验班提优训练八年级数学上册人教版》

例2 (2024·江苏扬州宝应期中)如图,∠AOB = 60°,C是BO延长线上的一点,OC = 8 cm,动点P从点C出发沿CB以3 cm/s的速度移动,动点Q从点O出发沿OA以2 cm/s的速度移动,如果点P,Q同时出发,用t(s)表示移动的时间,当t为( )s时,△POQ是等腰三角形。

A. $\frac{8}{5}$ B. 6 C. $\frac{8}{5}$或6 D. $\frac{8}{5}$或8
解析 分两种情况：(1)当点P在线段OC上时,设t s后△POQ是等腰三角形,
有OP = OC - CP = OQ,
即8 - 3t = 2t,解得t = $\frac{8}{5}$；
(2)当点P在CO的延长线上时,t ＞ $\frac{8}{3}$。
当△POQ是等腰三角形时,
∵∠AOB = 60°,
∴△POQ是等边三角形,∴OP = OQ,
即2t = 3t - 8,解得t = 8。
答案 D

答案： D

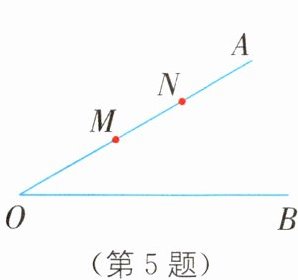
5. (2024·邯郸十三中二模)如图,M,N是∠AOB的边OA上的两个点(OM ＜ ON),∠AOB = 30°,OM = a,MN = 4,若边OB上有且只有1个点P,满足△PMN是等腰三角形,则a的取值范围是______。
甲答：a ＞ 8；乙答：a = 4,则正确的是( )。

A.只有甲对
B.只有乙对
C.甲、乙答案合一起才完整
D.甲、乙答案合一起也不对

答案：
C　[解析]①如图，作线段MN的垂直平分线交OB于点P，连接PM,PN.
　　　　　　
则PM=PN,此时△PMN是等腰三角形.过点M作MH⊥OB于点H，当MH＞MN时，满足条件的点P恰好只有一个.
∵MN=4,∠AOB=30°，当MH=4时,OM=2MH=8，
∴当a＞8时，满足条件的点P恰好只有一个；②当△PMN是等边三角形时，满足条件的点P恰好只有一个，此时MN=MP,∠NMP=60°.
∵∠AOB=30°，
∴∠MPO=30°，
∴OM=MP=MN=4，
∴a=4.综上所述，满足条件的a的取值范围是a = 4或a＞8.故选C.

6. 如图,直线a,b交于点O,∠α = 40°,点A是直线a上的一个定点,点B在直线b上运动,且始终位于直线a的上方,若以点O,A,B为顶点的三角形是等腰三角形,则∠OAB = ______。

答案：
40°或70°或100°　[解析]要使△OAB为等腰三角形，分三种情况讨论：
　　　　　　
①当OB₁=AB₁时，∠OAB₁=∠α=40°；②当OA=AB₂时，∠OAB₂=180°−2×40°=100°；③当OA=OB₃时，∠OAB₃=∠OB₃A=$\frac{1}{2}$×(180°−40°)=70°.综上所述，∠OAB的度数是40°或70°或100°.

例1 (2025·福建福州台江区期末)小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( )

解析 如图,作点A关于街道的对称点A',连接A'B交街道所在直线于点C,

∴A'C = AC,∴AC + BC = A'B。
在街道上任取除点C以外的一点C',连接A'C',BC',AC',
∴AC' + BC' = A'C' + BC'。
∵在△A'C'B中,两边之和大于第三边,
∴A'C' + BC' ＞ A'B,
∴AC' + BC' ＞ AC + BC,
∴点C到两小区送奶站距离之和最小。

答案 C
点拨 本题考查轴对称——最短路线的问题,将折线最短问题转化为“两点之间,线段最短”问题。会作对称点是解此类问题的基础,要求学生能熟练掌握,并熟练应用。另外本题的解决还应用了三角形的三边关系：三角形的两边之和大于第三边。

答案： C