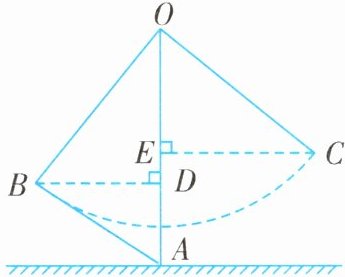
例1 (2025·山东泰安岱岳区期末)小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置$A$处,$OA$与地面垂直,两脚在地面上用力一蹬,妈妈在距地面$1m高的B$处接住她后用力一推,爸爸在$C$处接住她.若妈妈与爸爸到$OA的水平距离BD$,$CE分别为1.4m和1.9m$,$\angle BOC= 90^{\circ}$,爸爸在$C$处接住小丽时,小丽距离地面的高度是( ).
A.$1m$
B.$1.5m$
C.$1.6m$
D.$1.9m$
解析 $\because\angle BOC= 90^{\circ}$,
$\therefore\angle BOD+\angle COE= 90^{\circ}$,
$\because BD\perp OA$,$\therefore\angle BOD+\angle OBD= 90^{\circ}$.
$\therefore\angle OBD= \angle COE$.
又$\angle ODB= \angle CEO= 90^{\circ}$,$OB= CD$,
$\therefore\triangle OBD\cong\triangle COE(AAS)$,
$\therefore OE= BD$,$OD= CE$.
$\because妈妈与爸爸到OA的水平距离BD$,$CE分别为1.4m和1.9m$,
$\therefore OE= 1.4m$,$OD= 1.9m$,
$\therefore DE= OD-OE= 1.9-1.4= 0.5(m)$.
$\because点B与地面距离为1m$,$\therefore AD= 1m$,
$\therefore AE= AD+DE= 1+0.5= 1.5(m)$,
即爸爸在$C$处接住小丽时,小丽距离地面的高度是$1.5m$.
答案 B
点拨
本题属于中考常考的一线三垂直模型,熟记同角的余角相等是解题的关键.

A.$1m$
B.$1.5m$
C.$1.6m$
D.$1.9m$
解析 $\because\angle BOC= 90^{\circ}$,
$\therefore\angle BOD+\angle COE= 90^{\circ}$,
$\because BD\perp OA$,$\therefore\angle BOD+\angle OBD= 90^{\circ}$.
$\therefore\angle OBD= \angle COE$.
又$\angle ODB= \angle CEO= 90^{\circ}$,$OB= CD$,
$\therefore\triangle OBD\cong\triangle COE(AAS)$,
$\therefore OE= BD$,$OD= CE$.
$\because妈妈与爸爸到OA的水平距离BD$,$CE分别为1.4m和1.9m$,
$\therefore OE= 1.4m$,$OD= 1.9m$,
$\therefore DE= OD-OE= 1.9-1.4= 0.5(m)$.
$\because点B与地面距离为1m$,$\therefore AD= 1m$,
$\therefore AE= AD+DE= 1+0.5= 1.5(m)$,
即爸爸在$C$处接住小丽时,小丽距离地面的高度是$1.5m$.
答案 B
点拨
本题属于中考常考的一线三垂直模型,熟记同角的余角相等是解题的关键.
答案:
【解析】:本题可根据同角的余角相等证明两个三角形全等,再利用全等三角形的性质求出小丽距离地面的高度。
1. 证明$\triangle OBD\cong\triangle COE$:
已知$\angle BOC = 90^{\circ}$,则$\angle BOD + \angle COE = 90^{\circ}$。
因为$BD\perp OA$,所以$\angle BOD + \angle OBD = 90^{\circ}$。
根据同角的余角相等,可得$\angle OBD = \angle COE$。
又因为$\angle ODB = \angle CEO = 90^{\circ}$,且$OB = OC$(秋千的绳长不变)。
在$\triangle OBD$和$\triangle COE$中,$\begin{cases}\angle OBD = \angle COE\\\angle ODB = \angle CEO\\OB = OC\end{cases}$,根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle OBD\cong\triangle COE$。
2. 求出$OE$和$OD$的长度:
由全等三角形的性质可知,全等三角形的对应边相等,因为$\triangle OBD\cong\triangle COE$,所以$OE = BD$,$OD = CE$。
已知妈妈与爸爸到$OA$的水平距离$BD$,$CE$分别为$1.4m$和$1.9m$,所以$OE = 1.4m$,$OD = 1.9m$。
3. 求出$DE$的长度:
$DE = OD - OE = 1.9 - 1.4 = 0.5m$。
4. 求出小丽距离地面的高度:
因为点$B$与地面距离为$1m$,即$AD = 1m$,而$AE = AD + DE$,所以$AE = 1 + 0.5 = 1.5m$,即爸爸在$C$处接住小丽时,小丽距离地面的高度是$1.5m$。
【答案】:B
1. 证明$\triangle OBD\cong\triangle COE$:
已知$\angle BOC = 90^{\circ}$,则$\angle BOD + \angle COE = 90^{\circ}$。
因为$BD\perp OA$,所以$\angle BOD + \angle OBD = 90^{\circ}$。
根据同角的余角相等,可得$\angle OBD = \angle COE$。
又因为$\angle ODB = \angle CEO = 90^{\circ}$,且$OB = OC$(秋千的绳长不变)。
在$\triangle OBD$和$\triangle COE$中,$\begin{cases}\angle OBD = \angle COE\\\angle ODB = \angle CEO\\OB = OC\end{cases}$,根据$AAS$(两角及其中一角的对边对应相等的两个三角形全等),可得$\triangle OBD\cong\triangle COE$。
2. 求出$OE$和$OD$的长度:
由全等三角形的性质可知,全等三角形的对应边相等,因为$\triangle OBD\cong\triangle COE$,所以$OE = BD$,$OD = CE$。
已知妈妈与爸爸到$OA$的水平距离$BD$,$CE$分别为$1.4m$和$1.9m$,所以$OE = 1.4m$,$OD = 1.9m$。
3. 求出$DE$的长度:
$DE = OD - OE = 1.9 - 1.4 = 0.5m$。
4. 求出小丽距离地面的高度:
因为点$B$与地面距离为$1m$,即$AD = 1m$,而$AE = AD + DE$,所以$AE = 1 + 0.5 = 1.5m$,即爸爸在$C$处接住小丽时,小丽距离地面的高度是$1.5m$。
【答案】:B
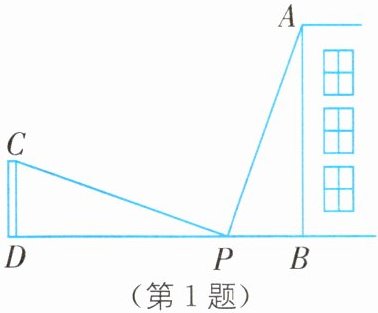
1.(2025·湖北武汉东湖开发区期末)如图,为了测量一幢高楼的高度,在木棍$CD与高楼AB之间选定一点P$,在点$P处用测角仪测得木棍顶端C的视线PC与地面的夹角\angle DPC= 19^{\circ}$,测得楼顶$A的视线PA与地面的夹角\angle BPA= 71^{\circ}$,量得点$P到楼底的距离PB$与木棍高度相等,都等于$5m$,量得木棍与高楼之间的距离$DB= 23m$,则高楼的高度是____$m$.

答案:
18 [解析]由题意,得CD⊥DB,AB⊥BD,
∴∠CDB=∠ABD=90°.
∵∠CPD=19°,
∴∠DCP=90°−∠CPD=71°.
∵∠APB=71°,
∴∠APB=∠DCP.
∵CD=PB=5m,
∴△CDP≌△PBA(ASA),
∴DP=AB,
∵BD=23m,
∴DP=AB=BD−PB=23−5=18(m),
∴高楼的高度是18m.
∴∠CDB=∠ABD=90°.
∵∠CPD=19°,
∴∠DCP=90°−∠CPD=71°.
∵∠APB=71°,
∴∠APB=∠DCP.
∵CD=PB=5m,
∴△CDP≌△PBA(ASA),
∴DP=AB,
∵BD=23m,
∴DP=AB=BD−PB=23−5=18(m),
∴高楼的高度是18m.
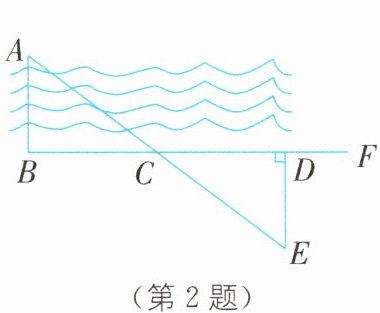
2.(2024·安徽滁州凤阳期末)如图,要测量河岸相对两点$A$,$B$的距离,已知$AB垂直于河岸BF$,先在$BF上取两点C$,$D$,使$CD= CB$,再过点$D作BF的垂线段DE$,使点$A$,$C$,$E$在一条直线上,测出$DE= 20$米,则$AB$的长是( ).
A.10米
B.15米
C.20米
D.25米

A.10米
B.15米
C.20米
D.25米
答案:
C [解析]
∵AB⊥BD,ED⊥BC,
∴∠ABC=∠EDC=90°.
在△ABC和△EDC中,∠ABC=∠EDC=90°,BC=DC,∠ACB=∠ECD,
∴△ABC≌△EDC(ASA),
∴AB=ED=20米.故选C.
∵AB⊥BD,ED⊥BC,
∴∠ABC=∠EDC=90°.
在△ABC和△EDC中,∠ABC=∠EDC=90°,BC=DC,∠ACB=∠ECD,
∴△ABC≌△EDC(ASA),
∴AB=ED=20米.故选C.
例2 (2024·山东潍坊期末)如图,在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ}$,$BC= 7cm$,$AC= 24cm$,$CD为AB$边上的高,直线$CD上一点F满足CF= AB$,点$E从点B出发在直线BC上以3cm/s$的速度移动,设运动时间为$t$秒,当$t= $____秒时,能使$\triangle ABC\cong\triangle CFE$.
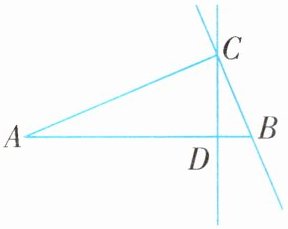
解析 如图,$\because\angle ACB= 90^{\circ}$,$CD\perp AB$,
$\therefore\angle BCD+\angle ACD= \angle A+\angle ACD= 90^{\circ}$,
$\therefore\angle A= \angle BCD$.
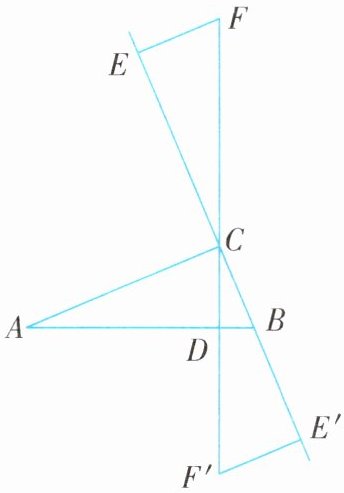
$\because\angle ECF= \angle BCD$,
$\therefore\angle ECF= \angle A$.
当$F在C$上方时,
$\because AB= CF$,$\angle A= \angle ECF$,
$\therefore当CE= AC= 24cm$时,$\triangle ABC\cong\triangle CFE$,
$\therefore BE= BC+CE= 7+24= 31(cm)$,
$\therefore t= \frac{31}{3}$;
当$F'在C$下方时,$\because CF'= AB$,$\angle BCD= \angle A$,$\therefore当CE'= AC= 24cm$时,$\triangle ABC\cong\triangle CF'E'$,$\therefore BE'= CE'-BC= 24-7= 17(cm)$,$\therefore t= \frac{17}{3}$,
$\therefore当t= \frac{17}{3}或\frac{31}{3}$时,能使$\triangle ABC\cong\triangle CFE$.
答案 $\frac{17}{3}或\frac{31}{3}$
点拨
解决动点中的全等问题,需要从运动的角度来考虑问题,在动中求静,在静中来解决问题.同时注意既然是运动的点,就需要考虑点运动的位置关系,由它运动的时间不同,构造的全等三角形的对应关系也不相同.

解析 如图,$\because\angle ACB= 90^{\circ}$,$CD\perp AB$,
$\therefore\angle BCD+\angle ACD= \angle A+\angle ACD= 90^{\circ}$,
$\therefore\angle A= \angle BCD$.

$\because\angle ECF= \angle BCD$,
$\therefore\angle ECF= \angle A$.
当$F在C$上方时,
$\because AB= CF$,$\angle A= \angle ECF$,
$\therefore当CE= AC= 24cm$时,$\triangle ABC\cong\triangle CFE$,
$\therefore BE= BC+CE= 7+24= 31(cm)$,
$\therefore t= \frac{31}{3}$;
当$F'在C$下方时,$\because CF'= AB$,$\angle BCD= \angle A$,$\therefore当CE'= AC= 24cm$时,$\triangle ABC\cong\triangle CF'E'$,$\therefore BE'= CE'-BC= 24-7= 17(cm)$,$\therefore t= \frac{17}{3}$,
$\therefore当t= \frac{17}{3}或\frac{31}{3}$时,能使$\triangle ABC\cong\triangle CFE$.
答案 $\frac{17}{3}或\frac{31}{3}$
点拨
解决动点中的全等问题,需要从运动的角度来考虑问题,在动中求静,在静中来解决问题.同时注意既然是运动的点,就需要考虑点运动的位置关系,由它运动的时间不同,构造的全等三角形的对应关系也不相同.
答案:
解:在$Rt\triangle ABC$中,$\angle ACB=90^{\circ}$,$CD\perp AB$,
$\therefore\angle BCD+\angle ACD=\angle A+\angle ACD=90^{\circ}$,
$\therefore\angle A=\angle BCD$,
$\because\angle ECF=\angle BCD$,
$\therefore\angle ECF=\angle A$。
当点$F$在点$C$上方时,
$\because AB=CF$,$\angle A=\angle ECF$,
$\therefore$当$CE=AC=24\space cm$时,$\triangle ABC\cong\triangle CFE(SAS)$,
$\because BC=7\space cm$,
$\therefore BE=BC+CE=7+24=31\space cm$,
$\because$点$E$的运动速度为$3\space cm/s$,
$\therefore t=\frac{31}{3}$。
当点$F$在点$C$下方时,
$\because CF=AB$,$\angle BCD=\angle A$,
$\therefore$当$CE=AC=24\space cm$时,$\triangle ABC\cong\triangle CF'E'(SAS)$,
$\therefore BE'=CE'-BC=24 - 7=17\space cm$,
$\therefore t=\frac{17}{3}$。
综上,$t=\frac{17}{3}$或$\frac{31}{3}$。
答案:$\frac{17}{3}$或$\frac{31}{3}$
$\therefore\angle BCD+\angle ACD=\angle A+\angle ACD=90^{\circ}$,
$\therefore\angle A=\angle BCD$,
$\because\angle ECF=\angle BCD$,
$\therefore\angle ECF=\angle A$。
当点$F$在点$C$上方时,
$\because AB=CF$,$\angle A=\angle ECF$,
$\therefore$当$CE=AC=24\space cm$时,$\triangle ABC\cong\triangle CFE(SAS)$,
$\because BC=7\space cm$,
$\therefore BE=BC+CE=7+24=31\space cm$,
$\because$点$E$的运动速度为$3\space cm/s$,
$\therefore t=\frac{31}{3}$。
当点$F$在点$C$下方时,
$\because CF=AB$,$\angle BCD=\angle A$,
$\therefore$当$CE=AC=24\space cm$时,$\triangle ABC\cong\triangle CF'E'(SAS)$,
$\therefore BE'=CE'-BC=24 - 7=17\space cm$,
$\therefore t=\frac{17}{3}$。
综上,$t=\frac{17}{3}$或$\frac{31}{3}$。
答案:$\frac{17}{3}$或$\frac{31}{3}$
查看更多完整答案,请扫码查看


