《2025年实验班提优训练八年级数学上册人教版》

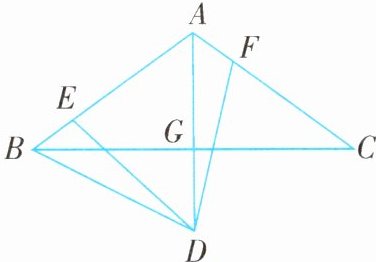
例6 (2025·河北秦皇岛昌黎期末)如图,在△ABC中,AB = AC,∠BAC = 120°,AD⊥BC,垂足为G,且AD = AB,∠EDF = 60°,其两边分别交边AB,AC于点E,F。
(1)求证：△ABD是等边三角形；
(2)求证：BE = AF。

名师启发 (1)由等腰三角形的性质和已知条件得出∠BAD = ∠DAC = $\frac{1}{2}$×120° = 60°,再由AD = AB,即可得出结论；
(2)由△ABD是等边三角形,得出BD = AD,∠ABD = ∠ADB = 60°,证出∠BDE = ∠ADF,由ASA证明△BDE ≌ △ADF,得出BE = AF。

答案：
(1)
∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC=$\frac{1}{2}$∠BAC.
∵∠BAC=120°,
∴∠BAD=∠DAC=$\frac{1}{2}$×120°=60°.
∵AD=AB,
∴△ABD是等边三角形.
(2)
∵△ABD是等边三角形,
∴∠ABD=∠ADB=60°,BD=AD.
∵∠EDF=60°,
∴∠ADB=∠EDF,
∴∠ADB−∠ADE=∠EDF−∠ADE,
∴∠BDE=∠ADF.在△BDE与△ADF中，$\begin{cases}∠DBE = ∠DAF = 60°\\BD = AD\\∠BDE = ∠ADF\end{cases}$
∴△BDE≌△ADF(ASA),
∴BE=AF.

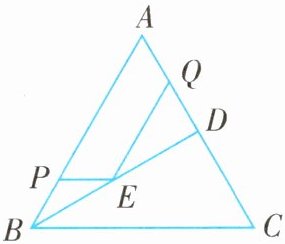
例7 (2025·四川广元苍溪期末)如图,在等边三角形ABC中,BD是中线,点P,Q分别在AB,AD上,且BP = AQ = QD = 1,动点E在BD上,则PE + QE的最小值为______。

名师启发 在BC上其一点P',使BP' = BP = 1,连接PP',P'Q,EP',证明出PE + QE的最小值为线段P'Q的长,△CP'Q是等边三角形,即可求出P'Q的长,从而解决问题。

答案：
3　[解析]如图,在BC上取一点P',使BP'=BP=1,连接PP',P'Q,EP'.
　　　　　　
∵△ABC是等边三角形,BD⊥AC于点D,
∴直线BD是△ABC的对称轴，点P'与点P关于BD对称,AC=2AD,
∴PE=P'E,
∴PE+QE=P'E+QE≥P'Q,
∴PE+QE的最小值为线段P'Q的长.
∵AQ=QD=1,
∴AC=2(AQ+QD)=2×2=4.
∵△ABC是等边三角形，
∴AC=BC,∠C=60°.
∵AQ=BP'=1,
∴CP'=CQ,
∴△CP'Q是等边三角形,
∴P'Q=CQ.
∵CQ=AC−AQ=4−1=3,
∴PE+QE的最小值为3.