《2025年实验班提优训练八年级数学上册人教版》

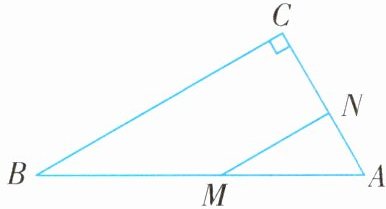
例4 如图,在Rt△ABC中,∠C = 90°,∠A = 60°,AB = 10 cm,若点M从点B出发以2 cm/s的速度向点A运动,点N从点A出发以1 cm/s的速度向点C运动,设M,N分别从点B,A同时出发,运动的时间为t s。
(1)用含t的式子表示线段AM,AN的长。
(2)当t为何值时,△AMN是以MN为底边的等腰三角形？
(3)当t为何值时,MN//BC？并求出此时CN的长。

解析 (1)根据点M和点N的运动速度分别表示出AM和AN即可；
(2)根据等腰三角形的定义得出AM = AN,列式计算即可；
(3)根据直角三角形中30°的角所对的直角边是斜边的一半,列式计算即可。
答案 (1)∵∠C = 90°,∠A = 60°,
∴∠B = 30°。
∵AB = 10 cm,
∴AM = AB - BM = 10 - 2t,AN = t。
(2)∵△AMN是以MN为底边的等腰三角形,
∴AM = AN,即10 - 2t = t,
∴当t = $\frac{10}{3}$时,△AMN是以MN为底边的等腰三角形。
(3)当MN⊥AC时,MN//BC。
∵∠C = 90°,∠A = 60°,∴∠B = 30°。
∵MN//BC,∴∠NMA = 30°,
∴AN = $\frac{1}{2}$AM,
∴t = $\frac{1}{2}$(10 - 2t),解得t = $\frac{5}{2}$,
∴当t = $\frac{5}{2}$时,MN//BC,
此时CN = 5 - $\frac{5}{2}$×1 = $\frac{5}{2}$。
方法技巧
解决动点问题一般分为两个环节：(1)确定动点的位置,在动态变化的过程中寻找可确定的因素(即可确定的量、可确定的位置)是突破问题的关键；利用几何图形的性质或图形变换的性质使动点和这些确定因素之间建立联系,从而确定或假定动点的位置,大多存在不同位置情况而进行分类；(2)解决问题：利用已经学过的等腰三角形的性质,全等三角形的性质和判定来解决问题。

答案：
(1)
∵∠C = 90°,∠A = 60°,
∴∠B = 30°。
∵AB = 10 cm,
∴AM = AB - BM = 10 - 2t,AN = t。
(2)
∵△AMN是以MN为底边的等腰三角形,
∴AM = AN,即10 - 2t = t,
∴当t = $\frac{10}{3}$时,△AMN是以MN为底边的等腰三角形。
(3)当MN⊥AC时,MN//BC。
∵∠C = 90°,∠A = 60°,
∴∠B = 30°。
∵MN//BC,
∴∠NMA = 30°,
∴AN = $\frac{1}{2}$AM,
∴t = $\frac{1}{2}$(10 - 2t),解得t = $\frac{5}{2}$,
∴当t = $\frac{5}{2}$时,MN//BC,此时CN = 5 - $\frac{5}{2}$×1 = $\frac{5}{2}$。

6. (2025·山东淄博张店区期末)如图,已知△ABC,点D为边BC上一点(点D不与点B,C重合)。
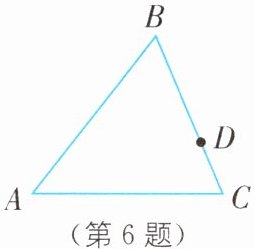
(1)尺规作图：作直线MN,使得点A与点D关于直线MN对称,直线MN交直线AC于M,交直线AB于N；(保留作图痕迹,不要求写作法)
(2)在(1)的基础上,连接DM,AD,AD交MN于点P。若已知AB + AC = 16,S_{△ABC} = 24,当MP = NP时,请求出点D到直线AC的距离。

答案：

(1)如图，直线MN为所求.
　　　　　　
(2)如图，过点D分别作DE⊥AB于点E，DF⊥AC于点F，由对称可知MN⊥AD.
∵MP=NP,
∴AM=AN,
∴∠PAM=∠PAN,
∴DE=DF.
∵$S_{\triangle ABD}=\frac{1}{2}AB\cdot DE$，$S_{\triangle ACD}=\frac{1}{2}AC\cdot DF$，
∴$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}=\frac{1}{2}(AB + AC)\cdot DF=\frac{1}{2}×16DF = 8DF$.
∵$S_{\triangle ABC}=24$，
∴$8DF = 24$，
∴$DF = 3$，
∴点D到直线AC的距离为3.