1. (2025·安徽淮北杜集区期中)在$\triangle ABC$中,$AD为BC$边的中线,若$\triangle ABD与\triangle ADC$的周长差为5,$AC = 8$,则$AB$的长为( ).
A.2
B.13
C.3或13
D.2或12
A.2
B.13
C.3或13
D.2或12
答案:
C [解析]①当△ABD的周长大于△ADC的周长时,由条件可知BD=CD,
∴△ABD与△ADC的周长差=(AB+AD+BD)−(AC+AD+CD)=AB−AC,
∴AB−8=5,解得AB=13;
②当△ADC的周长大于△ABD的周长时,
∵AD为边BC的中线,
∴BD=CD,
∴△ADC与△ABD的周长差=(AC+AD+CD)−(AB+AD+BD)=AC−AB.
∵△ABD与△ADC的周长差为5,AC=8,
∴8−AB=5,解得AB=3.
综上,AB=3或13.故选C.
∴△ABD与△ADC的周长差=(AB+AD+BD)−(AC+AD+CD)=AB−AC,
∴AB−8=5,解得AB=13;
②当△ADC的周长大于△ABD的周长时,
∵AD为边BC的中线,
∴BD=CD,
∴△ADC与△ABD的周长差=(AC+AD+CD)−(AB+AD+BD)=AC−AB.
∵△ABD与△ADC的周长差为5,AC=8,
∴8−AB=5,解得AB=3.
综上,AB=3或13.故选C.
2. 长度为20厘米的木棍,截成三段,每段长度为整数厘米,请写出一种可以构成三角形的截法,此时三段长度分别为____,能构成三角形的截法共有____种. (只考虑三段木棍的长度)
答案:
9厘米、9厘米、2厘米(答案不唯一) 8
[解析]
∵木棍的长度为20厘米,即三角形的周长为20厘米,由三边关系知最长边最大为9厘米,
∴①当三角形的最长边为9厘米时,有4种截法,分别是9厘米、9厘米、2厘米;9厘米、8厘米、3厘米;9厘米、7厘米、4厘米;9厘米、6厘米、5厘米.
②当三角形的最长边为8厘米时,有3种截法,分别是8厘米、8厘米、4厘米;8厘米、7厘米、5厘米;8厘米、6厘米、6厘米.
③当三角形的最长边为7厘米时,有1种截法,是7厘米、7厘米、6厘米,
∴能构成三角形的截法共有4+3+1=8(种).
[解析]
∵木棍的长度为20厘米,即三角形的周长为20厘米,由三边关系知最长边最大为9厘米,
∴①当三角形的最长边为9厘米时,有4种截法,分别是9厘米、9厘米、2厘米;9厘米、8厘米、3厘米;9厘米、7厘米、4厘米;9厘米、6厘米、5厘米.
②当三角形的最长边为8厘米时,有3种截法,分别是8厘米、8厘米、4厘米;8厘米、7厘米、5厘米;8厘米、6厘米、6厘米.
③当三角形的最长边为7厘米时,有1种截法,是7厘米、7厘米、6厘米,
∴能构成三角形的截法共有4+3+1=8(种).
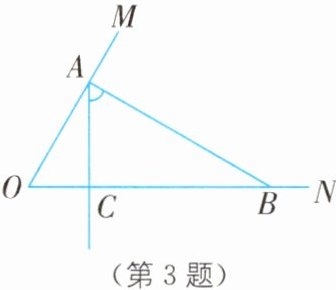
3. (2025·江西南昌期中)如图,已知$\angle MON = 60^{\circ}$,在射线$OM上取一点A$,过点$A作AB\perp OM交ON于点B$,以$A为端点画射线交线段OB于点C$(点$C不与点O$、点$B$重合). 若$\triangle AOC$中,有一个内角度数是另一个内角度数的2倍,则$\angle ACB$的度数是____.

答案:
90°或100°或140° [解析]
∵∠MON=60°,AB⊥OM,
∴∠OAB=90°,
∴∠ABC=30°.
①当∠AOC是∠OAC的2倍时,
则∠OAC=30°,
∴∠ACO=180°−∠AOC−∠OAC=90°,
∴∠ACB=180°−∠ACO=90°;
②当∠AOC是∠ACO的2倍时,∠ACO=30°,则点C与点B重合,不符合题意;
③当∠OAC是∠ACO的2倍时,
则∠OAC+∠ACO=3∠ACO=180°−∠AOB=120°,
∴∠OAC=80°,∠ACO=40°,
∴∠ACB=180°−∠ACO=140°;
④当∠ACO是∠OAC的2倍时,
则∠OAC+∠ACO=3∠OAC=180°−∠AOB=120°,
∴∠OAC=40°,∠ACO=80°,
∴∠ACB=180°−∠ACO=100°.
综上,∠ACB的度数为90°或100°或140°.
∵∠MON=60°,AB⊥OM,
∴∠OAB=90°,
∴∠ABC=30°.
①当∠AOC是∠OAC的2倍时,
则∠OAC=30°,
∴∠ACO=180°−∠AOC−∠OAC=90°,
∴∠ACB=180°−∠ACO=90°;
②当∠AOC是∠ACO的2倍时,∠ACO=30°,则点C与点B重合,不符合题意;
③当∠OAC是∠ACO的2倍时,
则∠OAC+∠ACO=3∠ACO=180°−∠AOB=120°,
∴∠OAC=80°,∠ACO=40°,
∴∠ACB=180°−∠ACO=140°;
④当∠ACO是∠OAC的2倍时,
则∠OAC+∠ACO=3∠OAC=180°−∠AOB=120°,
∴∠OAC=40°,∠ACO=80°,
∴∠ACB=180°−∠ACO=100°.
综上,∠ACB的度数为90°或100°或140°.
例2 已知在$\triangle ABC$中,$\angle A$,$\angle B$,$\angle C的对边分别为a$,$b$,$c$.
(1)化简代数式:$|a + b - c| + |b - a - c| = $____;
(2)若$AB = AC$,$AC边上的中线BD$把三角形的周长分为10和18两部分,求腰长$AB$.
解答 (1)$2a$
(2)画出图形如下:
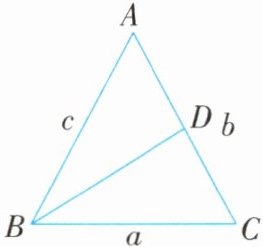
由题意可知,$BC = a$,$AC = b$,$AB = c$.
$\because AB = AC$,$\therefore b = c$.
$\because BD是AC$边上的中线,且$AC = b$,
$\therefore$分以下两种情况:
①当$\begin{cases}AB + AD = 10,\\BC + CD = 18\end{cases} $时,
即$\begin{cases}c + \dfrac{c}{2} = 10,\\a + \dfrac{c}{2} = 18\end{cases} 解得\begin{cases}a = \dfrac{44}{3},\\c = \dfrac{20}{3}\end{cases} $
此时$\triangle ABC的三边长分别为\dfrac{44}{3}$,$\dfrac{20}{3}$,$\dfrac{20}{3}$,不满足三角形的三边关系定理,舍去;
②当$\begin{cases}AB + AD = 18,\\BC + CD = 10\end{cases} $时,
即$\begin{cases}c + \dfrac{c}{2} = 18,\\a + \dfrac{c}{2} = 10\end{cases} 解得\begin{cases}c = 12,\\a = 4\end{cases} $
此时$\triangle ABC$的三边长分别为4,12,12,满足三角形的三边关系定理.
综上,腰长$AB$为12.
(1)化简代数式:$|a + b - c| + |b - a - c| = $____;
(2)若$AB = AC$,$AC边上的中线BD$把三角形的周长分为10和18两部分,求腰长$AB$.
解答 (1)$2a$
(2)画出图形如下:

由题意可知,$BC = a$,$AC = b$,$AB = c$.
$\because AB = AC$,$\therefore b = c$.
$\because BD是AC$边上的中线,且$AC = b$,
$\therefore$分以下两种情况:
①当$\begin{cases}AB + AD = 10,\\BC + CD = 18\end{cases} $时,
即$\begin{cases}c + \dfrac{c}{2} = 10,\\a + \dfrac{c}{2} = 18\end{cases} 解得\begin{cases}a = \dfrac{44}{3},\\c = \dfrac{20}{3}\end{cases} $
此时$\triangle ABC的三边长分别为\dfrac{44}{3}$,$\dfrac{20}{3}$,$\dfrac{20}{3}$,不满足三角形的三边关系定理,舍去;
②当$\begin{cases}AB + AD = 18,\\BC + CD = 10\end{cases} $时,
即$\begin{cases}c + \dfrac{c}{2} = 18,\\a + \dfrac{c}{2} = 10\end{cases} 解得\begin{cases}c = 12,\\a = 4\end{cases} $
此时$\triangle ABC$的三边长分别为4,12,12,满足三角形的三边关系定理.
综上,腰长$AB$为12.
答案:
(1)2a
(2)画出图形如下:
∵AB = AC,
∴b = c.
∵BD是AC边上的中线,且AC = b,
∴分以下两种情况:
①当$\begin{cases}AB + AD = 10,\\BC + CD = 18\end{cases} $时,
即$\begin{cases}c + \dfrac{c}{2} = 10,\\a + \dfrac{c}{2} = 18\end{cases} $解得$\begin{cases}a = \dfrac{44}{3},\\c = \dfrac{20}{3}\end{cases} $
此时$\triangle ABC$的三边长分别为$\dfrac{44}{3}$,$\dfrac{20}{3}$,$\dfrac{20}{3}$,不满足三角形的三边关系定理,舍去;
②当$\begin{cases}AB + AD = 18,\\BC + CD = 10\end{cases} $时,
即$\begin{cases}c + \dfrac{c}{2} = 18,\\a + \dfrac{c}{2} = 10\end{cases} $解得$\begin{cases}c = 12,\\a = 4\end{cases} $
此时$\triangle ABC$的三边长分别为4,12,12,满足三角形的三边关系定理.
综上,腰长$AB$为12.
(1)2a
(2)画出图形如下:
∵AB = AC,
∴b = c.
∵BD是AC边上的中线,且AC = b,
∴分以下两种情况:
①当$\begin{cases}AB + AD = 10,\\BC + CD = 18\end{cases} $时,
即$\begin{cases}c + \dfrac{c}{2} = 10,\\a + \dfrac{c}{2} = 18\end{cases} $解得$\begin{cases}a = \dfrac{44}{3},\\c = \dfrac{20}{3}\end{cases} $
此时$\triangle ABC$的三边长分别为$\dfrac{44}{3}$,$\dfrac{20}{3}$,$\dfrac{20}{3}$,不满足三角形的三边关系定理,舍去;
②当$\begin{cases}AB + AD = 18,\\BC + CD = 10\end{cases} $时,
即$\begin{cases}c + \dfrac{c}{2} = 18,\\a + \dfrac{c}{2} = 10\end{cases} $解得$\begin{cases}c = 12,\\a = 4\end{cases} $
此时$\triangle ABC$的三边长分别为4,12,12,满足三角形的三边关系定理.
综上,腰长$AB$为12.
查看更多完整答案,请扫码查看


