《2025年实验班提优训练八年级数学上册人教版》

2.下列命题：①有两个角和第三个角的平分线对应相等的两个三角形全等；②有两条边和第三条边上的中线对应相等的两个三角形全等；③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是( ).

A.①②
B.②③
C.①③
D.①②③

答案：
A　[解析]①正确，可以用AAS或者ASA定理判定两个三角形全等；②正确，可以用“倍长中线法”，用SAS定理判断两个三角形全等，如图,分别延长AD,A'D'到点E,E',使得AD=DE,A'D'=D'E',连接BE,B'E'.
∵AD=A'D',
∴AE=A'E'
易证△ADC≌△EDB,
∴BE=AC,∠E=∠DAC.
同理可得B'E'=A'C',∠E'=∠D'A'C'又AC=A'C',
∴BE=B'E',
又AB=A'B',
∴△ABE≌△A'B'E'(SSS),
∴∠BAE=∠B'A'E',∠E=∠E',
∴∠CAD=∠C'A'D',
∴∠BAC=∠B'A'C’
∴△BAC≌△B'A'C'(SAS).
③不正确，因为这个高可能在三角形的内部，也有可能在三角形的外部.故选A.

易错警示：本题中第②个命题需要等倍延长中线才能正确作出判断，第③个命题如果只考虑到三角形的高在三角形内，也容易判断错误.

3.(2024·湖北十堰期中)在如图所示$3×3$的小正方形组成的网格中,$\triangle ABC$的三个顶点分别在小正方形的顶点(格点)上,这样的三角形叫做格点三角形,图中能画出与$\triangle ABC$全等的格点三角形的个数为( ).


A.3
B.4
C.7
D.8

答案：
C　[解析]如图所示.有△ABD,△AMQ,△ANQ,△EQK,△FQK,△BTK,△BYK,共1+2+2+2=7个.故选C.

例2 (2024·浙江湖州吴兴区期末)如图,$\angle ABC= \angle DCB$.下列条件不能证明$\triangle ABC\cong\triangle DCB$的是( ).

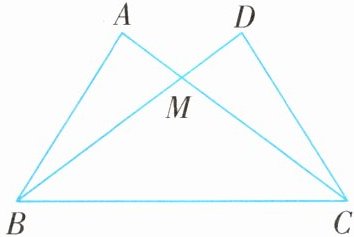
A.$AB= DC$
B.$\angle A= \angle D$
C.$BM= CM$
D.$AC= DB$

解析 在$\triangle ABC和\triangle DCB$中,
$\begin{cases}AB= DC,\\\angle ABC= \angle DCB,\\BC= CB,\end{cases} $
$\therefore\triangle ABC\cong\triangle DCB(SAS)$,
故A选项不符合题意；
在$\triangle ABC和\triangle DCB$中,$\begin{cases}\angle A= \angle D,\\\angle ABC= \angle DCB,\\BC= CB,\end{cases} $
$\therefore\triangle ABC\cong\triangle DCB(AAS)$,
故B选项不符合题意；
$\because BM= CM$,$\therefore\angle ACB= \angle DBC$.
在$\triangle ABC和\triangle DCB$中,$\begin{cases}\angle ABC= \angle DCB,\\BC= CB,\\\angle ACB= \angle DBC,\end{cases} $
$\therefore\triangle ABC\cong\triangle DCB(ASA)$,故C选项不符合题意；$SSA$不能证明三角形全等,故D选项符合题意.
答案 D

答案： 【解析】：
本题可根据全等三角形的判定定理，逐一分析各个选项能否证明$\triangle ABC\cong\triangle DCB$。
全等三角形有以下$5$个判定定理：
$SSS$（边边边）：三边对应相等的的三角形是全等三角形。
$SAS$（边角边）：两边及其夹角对应相等的三角形是全等三角形。
$ASA$（角边角）：两角及其夹边相等的三角形全等。
$AAS$（角角边）：两角及其一角的对边相等的三角形全等。
$HL$（斜边、直角边）：在一对直角三角形中，斜边及其另一条直角边相等的三角形全等。
选项A：$AB = DC$
在$\triangle ABC$和$\triangle DCB$中，已知$\angle ABC = \angle DCB$，$BC = CB$（公共边），再加上$AB = DC$，满足全等三角形判定定理中的$SAS$（两边及其夹角对应相等的三角形是全等三角形），所以能证明$\triangle ABC\cong\triangle DCB$，该选项不符合题意。
选项B：$\angle A = \angle D$
在$\triangle ABC$和$\triangle DCB$中，已知$\angle ABC = \angle DCB$，$BC = CB$（公共边），再加上$\angle A = \angle D$，满足全等三角形判定定理中的$AAS$（两角及其一角的对边相等的三角形全等），所以能证明$\triangle ABC\cong\triangle DCB$，该选项不符合题意。
选项C：$BM = CM$
因为$BM = CM$，根据等腰三角形的性质“等边对等角”，可得$\angle ACB = \angle DBC$。
在$\triangle ABC$和$\triangle DCB$中，已知$\angle ABC = \angle DCB$，$BC = CB$（公共边），再加上$\angle ACB = \angle DBC$，满足全等三角形判定定理中的$ASA$（两角及其夹边相等的三角形全等），所以能证明$\triangle ABC\cong\triangle DCB$，该选项不符合题意。
选项D：$AC = DB$
$SSA$（两边和其中一边的对角对应相等）不能证明三角形全等，在$\triangle ABC$和$\triangle DCB$中，$AC = DB$，$\angle ABC = \angle DCB$，$BC = CB$，属于$SSA$的情况，所以不能证明$\triangle ABC\cong\triangle DCB$，该选项符合题意。
【答案】：D

4.下列条件中,不能确定$\triangle ABC$的形状和大小的是( ).

A.$AB= 5$,$BC= 6$,$AC= 7$
B.$AB= 5$,$BC= 6$,$\angle B= 45^{\circ}$
C.$AB= 5$,$AC= 4$,$\angle B= 45^{\circ}$
D.$AB= 5$,$AC= 4$,$\angle C= 90^{\circ}$

答案： C　[解析]当AB=5,BC=6,AC=7时,根据SSS,可以得到△ABC是确定的，故选项A不符合题意;当AB=5,BC=6,∠B=45°时，根据SAS,可以得到△ABC是确定的，故选项B不符合题意;当AB=5,AC=4,∠B=45°时，无法确定△ABC,故选项C 符合题意;当AB=5,AC=4,∠C=90°时,根据HL可以得到△ABC是确定的，故选项D不符合题意,故选C.
归纳总结：已知三角形的三个元素，如果能用全等三角形的判定定理来进行判断，则这个三角形就能确定.

5.(2024·山东临沂期末)下列条件中,不能判定$\triangle ABC与\triangle DEF$一定全等的是( ).


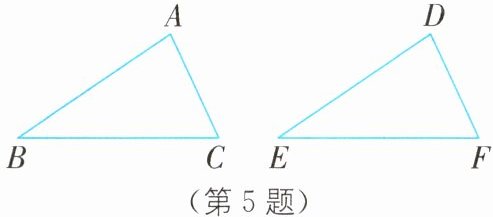
A.$AB= DE$,$BC= EF$,$\angle A= \angle D= 90^{\circ}$
B.$AB= DE$,$BC= EF$,$\angle A= \angle D= 80^{\circ}$
C.$AB= DE$,$\angle A= \angle D= 90^{\circ}$,$\angle B= \angle E= 40^{\circ}$
D.$BC= EF$,$\angle A= \angle D= 80^{\circ}$,$\angle B= \angle E= 40^{\circ}$

答案： B　[解析]A.
∵AB=DE,BC=EF,∠A=∠D=90°,
∴根据HL证明Rt△ABC≌Rt△DEF,不符合题意;B.
∵AB=DE,BC=EF,∠A=∠D=80°,根据SSA不能推出△ABC≌△DEF,故本选项符合题意;C.
∵AB=DE,∠A=∠D=90°,∠B=∠E=40°,
∴利用ASA能推出△ABC≌△DEF,故本选项不符合题意;D.
∵BC=EF,∠A=∠D=80°,∠B=∠E=40°,
∴利用AAS能推出△ABC≌△DEF,故本选项不符合题意,故选B.