《2025年智趣暑假作业七年级合订本》

1. 满足下列条件的两个三角形不一定全等的是(C)
A.有一边相等的两个等边三角形
B.有一腰和底边对应相等的两个等腰三角形
C.周长相等的两个三角形
D.斜边和一条直角边对应相等的两个等腰直角三角形

答案： C

2. 如图,$∠E= ∠F= 90^{\circ },∠B= ∠C,AE= AF$,结论：①$EM= FN;$②$CD= DN$；③$∠FAN= ∠EAM$；④$△ACN\cong △ABM$.其中正确的有(C)
A.1个
B.2个
C.3个
D.4个

答案： 解：
在△AEB和△AFC中，
∵∠E=∠F=90°，∠B=∠C，AE=AF，
∴△AEB≌△AFC（AAS），
∴∠EAB=∠FAC，AB=AC，BE=CF，
∴∠EAB-∠CAB=∠FAC-∠CAB，即∠EAM=∠FAN（③正确）。
在△AEM和△AFN中，
∵∠E=∠F=90°，AE=AF，∠EAM=∠FAN，
∴△AEM≌△AFN（ASA），
∴EM=FN（①正确），AM=AN。
在△ACN和△ABM中，
∵AC=AB，∠CAN=∠BAM，AN=AM，
∴△ACN≌△ABM（SAS）（④正确）。
无法证明CD=DN（②错误）。
综上，正确的有①③④，共3个。
答案：C

3. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知$AB= AC$,现添加以下的哪个条件仍不能判定$△ABE\cong △ACD$(D)
A.$∠B= ∠C$
B.$AD= AE$
C.$BD= CE$
D.$BE= CD$

答案： 解：已知 $AB = AC$，$\angle A$ 为 $\triangle ABE$ 和 $\triangle ACD$ 的公共角。
选项 A：若 $\angle B = \angle C$，则由“ASA”可判定 $\triangle ABE \cong \triangle ACD$。
- 选项 B：若 $AD = AE$，则由“SAS”可判定 $\triangle ABE \cong \triangle ACD$。
- 选项 C：若 $BD = CE$，则 $AB - BD = AC - CE$，即 $AD = AE$，由“SAS”可判定 $\triangle ABE \cong \triangle ACD$。
- 选项 D：若 $BE = CD$，仅满足“SSA”，不能判定 $\triangle ABE \cong \triangle ACD$。
答案：D

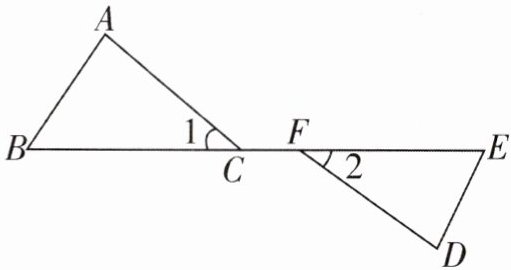
1. 如图所示,点B,C,F,E在同一直线上,$BC= FE$,$∠1= ∠2$,$∠1$不是(填“是”或“不是”)$∠2$的对顶角,若要使$△ABC\cong △DEF$,还需添加一个条件,这个条件可以是$AC=DF$(只需写出一个).

答案： 不是 $AC=DF$