2025年智趣暑假作业七年级合订本
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年智趣暑假作业七年级合订本 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
1. 下列命题中是真命题的是 (
A.相等的角是对顶角
B.同旁内角相等,两直线平行
C.同角的余角相等
D.如果$|a|= |b|$,那么$a= b$
C
)A.相等的角是对顶角
B.同旁内角相等,两直线平行
C.同角的余角相等
D.如果$|a|= |b|$,那么$a= b$
答案:
C
2. 已知三条不同的直线$a,b,c$在同一平面内,下列四个命题,是假命题的有 (
①如果$a// b,a⊥c$,那么$b⊥c$;②如果$b// a,c// a$,那么$b// c$;③如果$b⊥a,c⊥a$,那么$b⊥c$;④如果$b⊥a,c⊥a$,那么$b// c$.
A.1个
B.2个
C.3个
D.4个
A
)①如果$a// b,a⊥c$,那么$b⊥c$;②如果$b// a,c// a$,那么$b// c$;③如果$b⊥a,c⊥a$,那么$b⊥c$;④如果$b⊥a,c⊥a$,那么$b// c$.
A.1个
B.2个
C.3个
D.4个
答案:
解:①如果$a// b$,$a\perp c$,那么$b\perp c$,真命题;
②如果$b// a$,$c// a$,那么$b// c$,真命题;
③如果$b\perp a$,$c\perp a$,那么$b// c$,假命题;
④如果$b\perp a$,$c\perp a$,那么$b// c$,真命题。
假命题有1个。
答案:A
②如果$b// a$,$c// a$,那么$b// c$,真命题;
③如果$b\perp a$,$c\perp a$,那么$b// c$,假命题;
④如果$b\perp a$,$c\perp a$,那么$b// c$,真命题。
假命题有1个。
答案:A
3. 如图,直线$AB// CD,AF交CD于点E,∠CEF= 140^{\circ }$,则$∠A$等于 (
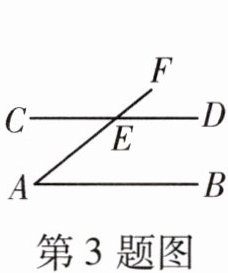
A.$35^{\circ }$
B.$40^{\circ }$
C.$45^{\circ }$
D.$50^{\circ }$
B
) 
A.$35^{\circ }$
B.$40^{\circ }$
C.$45^{\circ }$
D.$50^{\circ }$
答案:
解:
∵∠CEF=140°,∠CEF+∠DEF=180°
∴∠DEF=180°-140°=40°
∵AB//CD
∴∠A=∠DEF=40°
答案:B
∵∠CEF=140°,∠CEF+∠DEF=180°
∴∠DEF=180°-140°=40°
∵AB//CD
∴∠A=∠DEF=40°
答案:B
4. 如图,把一张长方形纸片沿$EF$折叠后,点$D,C分别落在D',C'$的位置. 若$∠EFB= 65^{\circ },∠AED'$等于 (
A.$70^{\circ }$
B.$65^{\circ }$
C.$50^{\circ }$
D.$25^{\circ }$
C
)A.$70^{\circ }$
B.$65^{\circ }$
C.$50^{\circ }$
D.$25^{\circ }$
答案:
解:
∵ 四边形ABCD是长方形,
∴ AD//BC,
∴ ∠DEF=∠EFB=65°(两直线平行,内错角相等)。
由折叠性质得∠D'EF=∠DEF=65°,
∴ ∠AED'=180°-∠DEF-∠D'EF=180°-65°-65°=50°。
答案:C
∵ 四边形ABCD是长方形,
∴ AD//BC,
∴ ∠DEF=∠EFB=65°(两直线平行,内错角相等)。
由折叠性质得∠D'EF=∠DEF=65°,
∴ ∠AED'=180°-∠DEF-∠D'EF=180°-65°-65°=50°。
答案:C
1. 对于命题“若$a^{2}>b^{2}$,则$a>b$”,举出能说明这个命题是假命题的一组$a,b$的值,则$a= $
$-2$
,$b= $$1$
.
答案:
要说明命题“若$a^{2}>b^{2}$,则$a>b$”是假命题,需找到一组$a$、$b$的值,使得$a^{2}>b^{2}$成立,但$a>b$不成立。
当$a = -2$,$b = 1$时:
$a^{2}=(-2)^{2}=4$,$b^{2}=1^{2}=1$,此时$a^{2}>b^{2}$($4>1$);
而$a=-2$,$b=1$,$-2<1$,即$a<b$,满足$a^{2}>b^{2}$但$a>b$不成立。
故答案为:$-2$;$1$。
当$a = -2$,$b = 1$时:
$a^{2}=(-2)^{2}=4$,$b^{2}=1^{2}=1$,此时$a^{2}>b^{2}$($4>1$);
而$a=-2$,$b=1$,$-2<1$,即$a<b$,满足$a^{2}>b^{2}$但$a>b$不成立。
故答案为:$-2$;$1$。
2. 如图,把一块三角板的$60^{\circ }$角的顶点放在直尺的一边上,若$∠1= 2∠2$,则$∠1= $
80
$^{\circ }$.
答案:
解:因为直尺两边平行,三角板60°角的顶点在直尺一边上,所以∠1与60°角的另一边和直尺另一边形成的角互补(两直线平行,同旁内角互补)。
由图可知,∠1 + (60° - ∠2) = 180°(平角定义),即∠1 - ∠2 = 120°。
又因为∠1 = 2∠2,所以2∠2 - ∠2 = 120°,解得∠2 = 120°,则∠1 = 2×120° = 240°(此步错误,重新分析)。
(正确分析)因为直尺两边平行,三角板60°角的一边与直尺一边重合,所以60°角的另一边与直尺另一边形成的角为∠2,且直尺的这条边与三角板的另一边形成∠1,根据两直线平行,同位角相等或内错角相等,可知∠1 + 60° + ∠2 = 180°(平角为180°)。
即∠1 + ∠2 = 120°,又∠1 = 2∠2,所以2∠2 + ∠2 = 120°,3∠2 = 120°,∠2 = 40°,则∠1 = 2×40° = 80°。
80
由图可知,∠1 + (60° - ∠2) = 180°(平角定义),即∠1 - ∠2 = 120°。
又因为∠1 = 2∠2,所以2∠2 - ∠2 = 120°,解得∠2 = 120°,则∠1 = 2×120° = 240°(此步错误,重新分析)。
(正确分析)因为直尺两边平行,三角板60°角的一边与直尺一边重合,所以60°角的另一边与直尺另一边形成的角为∠2,且直尺的这条边与三角板的另一边形成∠1,根据两直线平行,同位角相等或内错角相等,可知∠1 + 60° + ∠2 = 180°(平角为180°)。
即∠1 + ∠2 = 120°,又∠1 = 2∠2,所以2∠2 + ∠2 = 120°,3∠2 = 120°,∠2 = 40°,则∠1 = 2×40° = 80°。
80
查看更多完整答案,请扫码查看


