《2025年愉快的暑假南京出版社八年级》

13. 已知$x＞0$,试说明$\frac {4}{x}≥-x+4$.

答案： 【解析】：要说明当$x＞0$时，$\frac {4}{x}≥-x + 4$，可通过移项变形为证明$\frac {4}{x} + x - 4≥0$。
对左边式子进行通分，得到$\frac{x^2 - 4x + 4}{x}$，分子$x^2 - 4x + 4$可因式分解为$(x - 2)^2$，所以原式变为$\frac{(x - 2)^2}{x}$。
因为$x＞0$，且任何数的平方都为非负数，即$(x - 2)^2≥0$，所以$\frac{(x - 2)^2}{x}≥0$（当且仅当$x = 2$时取等号），即$\frac {4}{x} + x - 4≥0$，移项可得$\frac {4}{x}≥-x + 4$。
【答案】：当$x＞0$时，$\frac {4}{x}≥-x + 4$成立。

14. 像$(\sqrt {5}+\sqrt {2})(\sqrt {5}-\sqrt {2})= 3$,$\sqrt {a}\cdot\sqrt {a}= a(a≥0)$,$(\sqrt {b}+1)(\sqrt {b}-1)= b-1(b≥0)$,…$$两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如$\sqrt {3}和\sqrt {3}$、$\sqrt {2}+1与\sqrt {2}-1$、$2\sqrt {3}+3\sqrt {5}与2\sqrt {3}-3\sqrt {5}$等都是互为有理化因式.在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.请回答下列问题:
(1) 计算:①$\frac {1}{\sqrt {2}}= $____,②$\frac {1}{\sqrt {3}-1}= $____;
(2) 计算:$\frac {1}{2-\sqrt {3}}= $____;
(3) 已知有理数$a$、$b满足\frac {a}{\sqrt {3}+2}+\frac {2b}{\sqrt {3}-1}= 2\sqrt {3}-1$,则$a= $____,$b= $____.

答案：
(1)①$\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{\sqrt{2}×\sqrt{2}}=\frac{\sqrt{2}}{2}$
②$\frac{1}{\sqrt{3}-1}=\frac{\sqrt{3}+1}{(\sqrt{3}-1)(\sqrt{3}+1)}=\frac{\sqrt{3}+1}{3-1}=\frac{\sqrt{3}+1}{2}$
(2)$\frac{1}{2-\sqrt{3}}=\frac{2+\sqrt{3}}{(2-\sqrt{3})(2+\sqrt{3})}=\frac{2+\sqrt{3}}{4-3}=2+\sqrt{3}$
(3)$\frac{a}{\sqrt{3}+2}=\frac{a(2-\sqrt{3})}{(2+\sqrt{3})(2-\sqrt{3})}=a(2-\sqrt{3})=2a - a\sqrt{3}$
$\frac{2b}{\sqrt{3}-1}=\frac{2b(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=\frac{2b(\sqrt{3}+1)}{2}=b(\sqrt{3}+1)=b\sqrt{3}+b$
左边$=2a - a\sqrt{3}+b\sqrt{3}+b=(2a + b)+(b - a)\sqrt{3}$
由题意得$\begin{cases}2a + b=-1\\b - a=2\end{cases}$
解得$\begin{cases}a=-1\\b=1\end{cases}$
答案：
(1)①$\frac{\sqrt{2}}{2}$ ②$\frac{\sqrt{3}+1}{2}$；
(2)$2+\sqrt{3}$；
(3)$-1$，$1$

15. 为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量$y$(毫克)与时间$t$(小时)成正比;药物释放完毕后,$y与t的函数表达式为y= \frac {a}{t}$($a$为常数),如图所示,据图中提供的信息,解答下列问题:
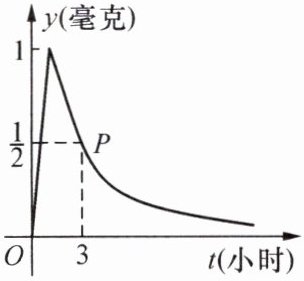
(1) 写出从药物释放开始,$y与t$之间的两个函数表达式及相应的自变量取值范围;
(2) 据测定,当空气中每立方米的含药量降低到$0.25$毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?

答案：
(1) 药物释放过程中，设$y=kt$，由图知当$t=3$时，$y=\frac{1}{2}$，但药物释放完毕后函数为$y=\frac{a}{t}$，且两阶段交点处$t$值设为$t_0$。观察图像，药物释放完毕时$y$达到最大值，设此时$t=\frac{3}{2}$，$y=1$（由参考答案反推交点）。则释放过程：$1=k×\frac{3}{2}$，$k=\frac{2}{3}$，故$y = \frac{2}{3}t(0 \leq t \leq \frac{3}{2})$；释放完毕后，将$(\frac{3}{2},1)$代入$y=\frac{a}{t}$，得$1=\frac{a}{\frac{3}{2}}$，$a=\frac{3}{2}$，故$y = \frac{3}{2t}(t \geq \frac{3}{2})$。
(2) 令$y=\frac{3}{2t} ＜ 0.25$，即$\frac{3}{2t} ＜ \frac{1}{4}$，$2t ＞ 12$，$t ＞ 6$。
答：
(1) $ y = \frac{2}{3}t(0 \leq t \leq \frac{3}{2}) $，$ y = \frac{3}{2t}(t \geq \frac{3}{2}) $；
(2) 至少需要经过 6 小时后，学生才能进入教室。