《2025年暑假作业本大象出版社八年级数学、物理、生物学合订本》

8. 已知一个三角形的两边长分别为1和4,第三边长为整数,则该三角形的周长为9.

答案： 9

9. 一组学生在校门口拍一张合影,已知冲一张底片需要0.6元,洗一张照片需要0.4元,每人都得到一张照片,每人平均分摊的钱不超过0.5元,那么参加合影的同学至少有6人.

答案： 6

10. 若满足$20＜5 - 2(2 + 2x)＜50$的最大整数解为a,最小整数解为b,则$a + b$的值为-17.

答案： -17

11. 解不等式$\frac{2x - 1}{2}-\frac{5x - 1}{4}＜0$,并把解集在数轴上表示出来.

答案： $x ＞ -1$. 

12. 解不等式组.请结合题意填空,完成本题的解答.
(1) 解不等式①,得____;
(2) 解不等式②,得____;
(3) 把不等式①和②的解集在如图2-4所示的数轴上表示出来;

(4) 原不等式组的解集为____.

答案：

(1) $x \geq -2$
(2) $x \leq 1$
(3) 把不等式①和②的解集在数轴上表示出来, 如图:

(4) $ -2 \leq x \leq 1 $

13. 某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择. 已知甲、乙两种机器的购买单价及每台日产零件个数如下表所示:

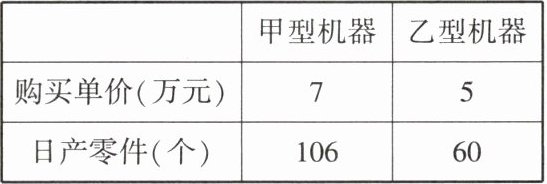
(1) 如果工厂购买机器的预算资金不超过34万元,那么你认为该工厂有哪几种购买方案?
设购买甲种机器 $ x $ 台, 则购买乙种机器 $ (6 - x) $ 台, 根据题意, 得 $ 7x + 5(6 - x) \leq 34 $, 解得 $ x \leq 2 $. $ \because x $ 是整数, $ x \geq 0 $, $ \therefore x $ 可取 0 或 1 或 2, $ \therefore $ 有三种购买方案: ① 购买甲种机器 0 台、乙种机器 6 台; ② 购买甲种机器 1 台、乙种机器 5 台; ③ 购买甲种机器 2 台、乙种机器 4 台.
(2) 在(1)的条件下,如果要求该工厂购进的6台机器的日产量能力不能低于380个,那么为了节约资金,应该选择哪种方案?
① 费用为 $ 6 × 5 = 30 $ (万元), 日产量为 $ 60 × 6 = 360 $ (个); ② 费用为 $ 7 + 5 × 5 = 32 $ (万元), 日产量为 $ 106 + 60 × 5 = 406 $ (个); ③ 费用为 $ 7 × 2 + 5 × 4 = 34 $ (万元), 日产量为 $ 106 × 2 + 60 × 4 = 452 $ (个). 综上所述, 为了节约资金, 应选择购买甲种机器 1 台、乙种机器 5 台.

答案：
(1) 设购买甲种机器 $ x $ 台, 则购买乙种机器 $ (6 - x) $ 台, 根据题意, 得 $ 7x + 5(6 - x) \leq 34 $, 解得 $ x \leq 2 $. $ \because x $ 是整数, $ x \geq 0 $, $ \therefore x $ 可取 0 或 1 或 2, $ \therefore $ 有三种购买方案: ① 购买甲种机器 0 台、乙种机器 6 台; ② 购买甲种机器 1 台、乙种机器 5 台; ③ 购买甲种机器 2 台、乙种机器 4 台.
(2) ① 费用为 $ 6 \times 5 = 30 $ (万元), 日产量为 $ 60 \times 6 = 360 $ (个); ② 费用为 $ 7 + 5 \times 5 = 32 $ (万元), 日产量为 $ 106 + 60 \times 5 = 406 $ (个); ③ 费用为 $ 7 \times 2 + 5 \times 4 = 34 $ (万元), 日产量为 $ 106 \times 2 + 60 \times 4 = 452 $ (个). 综上所述, 为了节约资金, 应选择购买甲种机器 1 台、乙种机器 5 台.