《2025年南通小题课时作业本八年级数学上册苏科版》

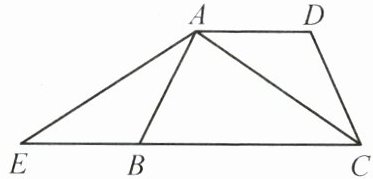
20. (8 分)如图,在四边形 $ ABCD $ 中,$ AB = DC $,延长 $ CB $ 到点 $ E $,使 $ BE = AD $,连接 $ AE $,$ AC $,且 $ AE = AC $,求证：$ AD // EC $.

答案： 证明:在△ABE和△CDA中，$\left\{\begin{array}{l} AE=CA\\ AB=CD\\ BE=DA\end{array}\right.$
所以△ABE≌△CDA(SSS)，所以∠E=∠CAD.
因为AE=AC，所以∠E=∠ACE，
所以∠ACE=∠CAD，所以AD//EC.

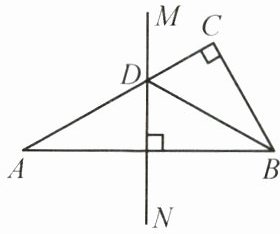
21. (8 分)(2024 南京秦淮期末)如图,在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AC = 8 $,$ AB $ 的垂直平分线 $ MN $ 交 $ AC $ 于点 $ D $,连接 $ BD $.
(1)若 $ \angle A = 25^{\circ} $,求 $ \angle DBC $ 的度数；
(2)若 $ BC = 4 $,求 $ BD $ 的长.

答案：
(1)因为MN垂直平分AB，
所以DA=DB，所以∠DBA=∠A=25°.
因为∠C=90°，
所以∠ABC=90°−25°=65°，
所以∠DBC=∠ABC−∠DBA=65°−25°=40°.
(2)设BD=x，则DA=x，所以CD=8−x，
在△BCD中，由勾股定理，得$BD^2=CD^2+BC^2$，
所以$x^2=(8−x)^2+4^2$，解得x=5，
所以BD=5.

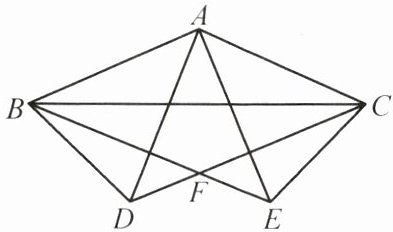
22. (8 分)(2024 南京鼓楼期末)如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ \triangle ADC $ 和 $ \triangle ABE $ 分别是以 $ AC $,$ AB $ 为腰的等腰直角三角形,$ BE $ 与 $ CD $ 相交于点 $ F $.
(1)求证：$ \angle FBC = \angle FCB $；
(2)连接 $ AF $,求证：$ AF \perp BC $.

答案：
(1)因为AB=AC，△ADC和△ABE分别是以AC,AB为腰的等腰直角三角形，
所以AD=AE=AB=AC，∠DAC=∠EAB=90°，
BE=CD，
所以∠DAB=90°−∠DAE=∠EAC，
所以△ABD≌△ACE(SAS)，
所以BD=CE.
因为CD=BE，BC=BC，
所以△BCD≌△CBE(SSS)，
所以∠BCD=∠CBE，
即∠FBC=∠FCB.
(2)由
(1)知，BF=FC.
因为AB=AC，
所以AF是BC的垂直平分线，
所以AF⊥BC.