8. 若一次函数$y = x + 5的图象经过点A(a,b)$,$B(c,d)$,则$a(c - d) + b(d - c)$等于( )
A.$0$
B.$20$
C.$25$
D.$-25$
A.$0$
B.$20$
C.$25$
D.$-25$
答案:
C
9. 若函数$y = kx + 3的图象经过点(2,5)$,则$k = $______.
答案:
1
10. 若将直线$y = -2x$向上平移4个单位长度,则平移后的直线的函数表达式是______.
答案:
y=-2x+4
11. (2024宁夏)在平面直角坐标系中,已知一条直线与两坐标轴围成的三角形是等腰三角形,则该直线的表达式可能为______.(写出一个即可)
答案:
y=x+1(答案不唯一)
12. 已知关于$x的一次函数y = (2a + 1)x + a - 2$,若$y随x$的增大而增大,且其图象与$y$轴的交点在原点下方,则实数$a$的取值范围是______.
答案:
-$\frac{1}{2}$<a<2
13. (2024徐州九里期末)如图,直线$y = 2x与y = kx + b相交于点P(1,2)$,则关于$x的方程kx + b = 2x$的解是______.


答案:
x=1
14. (2025南京鼓楼月考)已知一次函数$y = mx - 4m$,当$1 \leq x \leq 3$时,$2 \leq y \leq 6$,则$m$的值为______.
答案:
-2
15. (2024南通)在平面直角坐标系$xOy$中,已知点$A(3,0)$,$B(0,3)$,直线$y = kx + b$($k$,$b$为常数,且$k > 0$)经过点$(1,0)$,并把$\triangle AOB$分成两部分,其中靠近原点部分的面积为$\frac{15}{4}$,则$k$的值为______.
答案:
$\frac{3}{5}$
16. 如图,一次函数$y = -2x + 4的图象与坐标轴分别交于A$,$B$两点,将线段$AB绕点A按逆时针方向旋转90^{\circ}$,点$B落在点B'$处,则点$B'$的坐标是______.


答案:
(4,6)
17. 如图,在平面直角坐标系中,一次函数$y = k(x - 1)的图象分别交x$轴,$y轴于A$,$B$两点,且$OB = 2OA$,将直线$AB绕点B按顺时针方向旋转45^{\circ}$,交$x轴于点C$,则直线$BC$的函数表达式是______.


答案:
y=$\frac{1}{3}$x-2
18. 如图,在平面直角坐标系$xOy$中,点$B的坐标为(-8,6)$,过点$B分别作x$轴,$y$轴的垂线,垂足分别为$C$,$A$,直线$y = -2x - 6与AB交于点D$,与$y轴交于点E$,动点$M在线段BC$上,动点$N在直线y = -2x - 6$上. 若$\triangle AMN是以N$为直角顶点的等腰直角三角形,则点$M$的坐标为______.
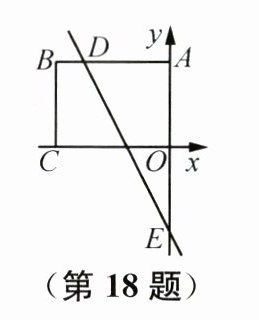

答案:
(-8,6)或$(-8,\frac{2}{3})$
查看更多完整答案,请扫码查看


