9. (2024无锡锡山月考)若不等边三角形的三边长分别是2,7,$x - 1$,则整数$x$的值是______。
答案:
7,8,9
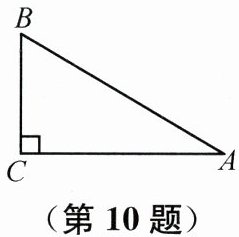
10. (2024盐城盐都月考)如图,$\angle A= 30^{\circ}$,$\angle C= 90^{\circ}$,$BC= 2$,则$AB$的长为______。

答案:
4
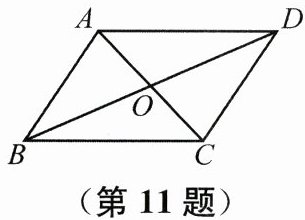
11. 如图,已知$AB= CD$,$AD= CB$,且$AB// CD$,$AD// BC$,$AC$,$BD相交于点O$,则图中共有______对全等三角形。

答案:
4
12. (2025扬州邗江期末)在等腰三角形$ABC$中,$\angle A= 2\angle B$,则$\angle C$的度数为______。
答案:
$45^{\circ}$或$72^{\circ}$
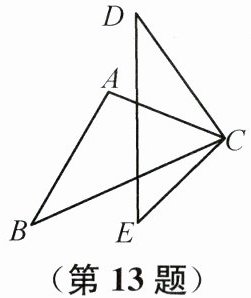
13. (2024成都)如图,$\triangle ABC\cong\triangle CDE$,若$\angle D= 35^{\circ}$,$\angle ACB= 45^{\circ}$,则$\angle DCE$的度数为______。

答案:
$100^{\circ}$
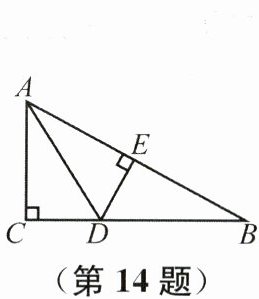
14. 如图,在$\triangle ABC$中,$\angle C= 90^{\circ}$,$D是BC$上的一点,$DE\perp AB于点E$,$AE= AC$,连接$AD$,若$BC= 8$,则$BD+DE$等于______。

答案:
8
15. (2024凉山州)如图,在$\triangle ABC$中,$\angle BCD= 30^{\circ}$,$\angle ACB= 80^{\circ}$,$CD是边AB$上的高,$AE是\angle CAB$的平分线,则$\angle AEB$的度数是______。
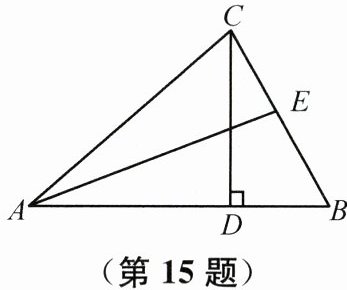

答案:
$100^{\circ}$
16. (2025南通海安期末)如图,在$\triangle ABC$中,$\angle A= 105^{\circ}$,$AC的垂直平分线MN交BC于点N$,且$AB+BN= BC$,则$\angle B$的度数是______。
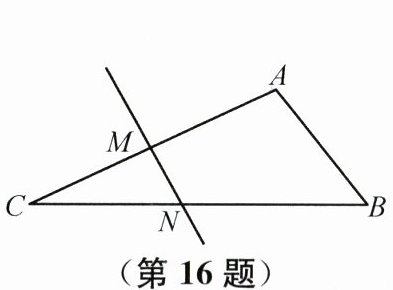

答案:
$50^{\circ}$
17. (2025南通如皋期末)如图,$BD是\triangle ABC$的角平分线,$AB= 6$,$BC= 4$,过点$D作DE\perp AB$,垂足为$E$。若$DE= 2$,则$\triangle ABC$的面积为______。
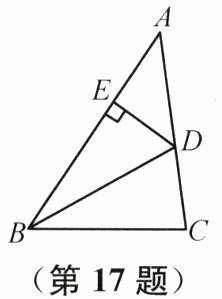

答案:
10
18. (2025宿迁泗洪期末)如图,$\triangle AOB和\triangle COD$是等腰直角三角形,$\angle AOB= \angle COD= 90^{\circ}$,连接$AD$,$BC$。若$OA= 1$,$OD= 2$,则四边形$ABCD$面积的最大值为______。
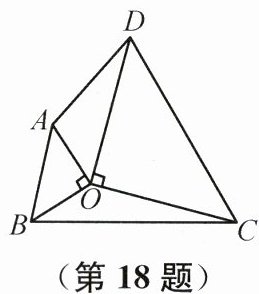

答案:
$\frac{9}{2}$
19. (6分)(2024攀枝花)如图,$AB// CD$,$AE// CF$,$BF= DE$,求证:$AB= CD$。
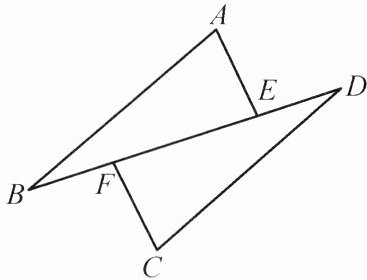

答案:
证明:因为$AB// CD$,$AE// CF$,所以$\angle B=\angle D$,$\angle AEB=\angle CFD$.因为$BF=DE$,所以$BE=DF$.在$\triangle ABE$与$\triangle CDF$中,$\left\{\begin{array}{l} \angle B=\angle D,\\ BE=DF,\\ \angle AEB=\angle CFD,\end{array}\right.$所以$\triangle ABE\cong \triangle CDF(ASA)$,所以$AB=CD$.
查看更多完整答案,请扫码查看


