《2025年南通小题课时作业本八年级数学上册苏科版》

24. (8分)(2025常熟模拟)甲、乙两名同事计划周末登“虞山”,两人从山下同一地点出发,相约$11:00$之前到达山顶某景区,甲先出发,中途在休息一段时间后保持原速继续登山；乙晚出发40分钟,比甲早到达山顶. 从$8:30$开始计时,时长记为$t\ min$,甲、乙两人登山的路程记为$y_{甲}$,$y_{乙}$. 甲、乙两人登山的路程$y_{甲}$,$y_{乙}与时长t$之间的函数关系如图所示.
(1)乙到达山顶的时间为______；
(2)记甲的速度为$v_1$,乙的速度为$v_2$.
①甲、乙两人的速度之比$\frac{v_1}{v_2}$的值为______；
②已知甲的速度$v_1 = 80m/min$,在甲登山的过程中,若$|y_{甲} - y_{乙}| = 2000$,求$t$的值.

答案：
(1)10:30
(2)①$\frac{2}{3}$②根据题意,得a=60×80=4800,$v_{2}=\frac{3v_{1}}{2}=\frac{3}{2}×80=120(m/min)$,则$y_{乙}=120(t-40)=120t-4800(40\leq t\leq120)$,易得当0≤t≤60时,$y_{甲}=80t$,所以|y$_{甲}$-y$_{乙}$|=80t-(120t-4800)=2000,解得t=70,舍去;当60＜t≤90时,$y_{甲}=4800$,所以|y$_{甲}$-y$_{乙}$|=|4800-(120t-4800)|=2000,解得t=$\frac{190}{3}$或t=$\frac{290}{3}$(舍去);当90＜t≤120时,$y_{甲}=4800+80(t-90)=80t-2400$,所以|y$_{甲}$-y$_{乙}$|=120t-4800-(80t-2400)=2000,解得t=110;当120＜t≤150时,$y_{乙}=9600$,所以|y$_{甲}$-y$_{乙}$|=9600-(80t-2400)=2000,解得t=125.综上,t的值为$\frac{190}{3}$或110或125.

25. (12分)(2025苏州高新月考)如图1,在平面直角坐标系中,$O$为坐标原点,点$A(-4,0)$,$AB // y$轴,点$C在y$轴上,一次函数$y = \frac{1}{4}x + 3的图象经过点B$,$C$.
(1)点$C$的坐标为______,点$B$的坐标为______；
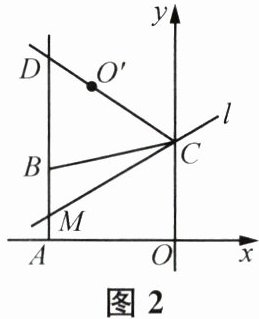
(2)如图2,直线$l经过点C$,且与直线$AB交于点M$,点$O'与点O关于直线l$对称,连接$CO'$并延长,交射线$AB于点D$.
①求证：$\triangle CMD$是等腰三角形；
②当$CD = 5$时,求直线$l$的函数表达式.

答案：
(1)(0,3) (-4,2)
(2)①证明:因为AB//y轴,所以∠OCM=∠CMD.因为∠OCM=∠MCD,所以∠CMD=∠MCD,所以MD=CD,所以△CMD是等腰三角形.②解:如图,过点D作DP⊥y轴于点P.在Rt△DCP中,由勾股定理,得CP=$\sqrt{CD^{2}-DP^{2}}=3$,所以OP=AD=CO+CP=3+3=6,所以AM=AD-DM=6-5=1,所以点M的坐标是(-4,1).设直线l的函数表达式为y=kx+b(k≠0),将点M(-4,1),C(0,3)分别代入,得$\begin{cases}1=-4k+b,\\3=b,\end{cases}$解得$\begin{cases}k=\frac{1}{2},\\b=3,\end{cases}$所以直线l的函数表达式为y=$\frac{1}{2}$x+3;当点D与点A重合时,直线l的函数表达式为y=2x+3.综上,直线l的函数表达式为y=$\frac{1}{2}$x+3或y=2x+3.