《2025年南通小题课时作业本八年级数学上册苏科版》

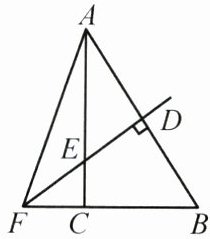
20. (8分)如图,在$\triangle ABC$中,$AB的垂直平分线分别交AB$,$AC及BC的延长线于点D$,$E$,$F$,且$CB^{2} = AE^{2} - CE^{2}$。
(1)求证：$\angle ACB = 90^{\circ}$；
(2)若$AC = 12$,$BC = 9$,求$CE$的长。

答案：
(1)连接BE.因为ED垂直平分AB,所以AE=BE;因为CB²=AE²−CE²,所以CB²=BE²−CE²,所以CB²+CE²=BE²,所以△BCE是直角三角形,所以∠ACB=90°.
(2)设CE=x,则AE=12−x.因为BE=AE,所以BE=12−x,在△BEC中,∠ECB=90°,BC=9,所以CB²+CE²=BE²,即9²+x²=(12−x)²,解得x=$\frac{21}{8}$,所以CE的长为$\frac{21}{8}$.

21. (8分)如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$。
(1)在线段$AC上找一点D$,使得点$D到AB$,$BC$的距离相等(要求：尺规作图,保留作图痕迹,不写作法)；
(2)连接$BD$,若$BC = 6$,$AB = 10$,求$AD$的长。

答案：
(1)如图，点D即为所求.
(2)过点D作DT⊥AB于点T.因为BD平分∠ABC,DC⊥BC,DT⊥BA,所以DC=DT;设DC=DT=x.在△ABC中,∠C=90°,BC=6,AB=10,所以AC=$\sqrt{AB^{2}-BC^{2}}=\sqrt{10^{2}-6^{2}}=8$.因为S△ABC=$\frac{1}{2}$AC·BC=$\frac{1}{2}$BC·DC+$\frac{1}{2}$·AB·DT,所以6×8=6x+10x,解得x=3,所以AD=AC−CD=8−3=5.