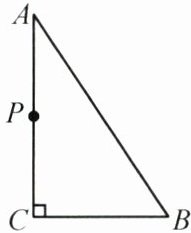
24. (8分)如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AB = 5cm$,$BC = 3cm$,若动点$P从点C$开始,按$C\to A\to B\to C$的路径运动,且速度为1cm/s,设出发的时间为$t s$。
(1)若$AP恰好是\angle BAC$的平分线,求$t$的值;
(2)问当$t$为何值时,$\triangle BCP$为等腰三角形?
(1)若$AP恰好是\angle BAC$的平分线,求$t$的值;
(2)问当$t$为何值时,$\triangle BCP$为等腰三角形?

答案:
(1)如图1,过点P作PE⊥AB,垂足为E.因为AP恰好是∠BAC的平分线,且∠C=90°,AB=5cm,BC=3cm,所以CP=EP,AC=4cm.又AP=AP,所以△ACP≌△AEP(HL),所以AE=AC=4cm,BE=5−4=1(cm).设CP=x,则BP=3−x,PE=x,所以在Rt△BEP中,BE²+PE²=BP²,即1²+x²=(3−x)²,解得x=$\frac{4}{3}$,所以BP=3−$\frac{4}{3}$=$\frac{5}{3}$(cm),所以CA+AB+BP=4+5+$\frac{5}{3}$=$\frac{32}{3}$(cm),此时t=$\frac{32}{3}$÷1=$\frac{32}{3}$.故t的值为$\frac{32}{3}$.
(2)如图2,当CP=CB时,△BCP为等腰三角形,若点P在CA上,则t=$\frac{3}{1}=3$;如图3,当BP=BC=3cm时,△BCP为等腰三角形,则AP=AB−BP=2cm,所以t=(4+2)÷1=6;如图4,若点P在AB上,CP=CB=3cm,过点C作CD⊥AB于点D,则根据直角三角形的面积法,得CD=$\frac{12}{5}$.在Rt△BCD中,由勾股定理,得BD=$\frac{9}{5}$,所以PB=2BD=$\frac{18}{5}$,所以CA+AP=4+5−$\frac{18}{5}=5.4$,此时t=5.4÷1=5.4;如图5,当PC=PB时,△BCP为等腰三角形,过点P作PD⊥BC于点D,则BD=CD,所以AP=BP=$\frac{1}{2}$AB=$\frac{5}{2}$,所以t=(4+$\frac{5}{2}$)÷1=6.5.综上所述,当t的值为3或5.4或6或6.5时,△BCP为等腰三角形.
(1)如图1,过点P作PE⊥AB,垂足为E.因为AP恰好是∠BAC的平分线,且∠C=90°,AB=5cm,BC=3cm,所以CP=EP,AC=4cm.又AP=AP,所以△ACP≌△AEP(HL),所以AE=AC=4cm,BE=5−4=1(cm).设CP=x,则BP=3−x,PE=x,所以在Rt△BEP中,BE²+PE²=BP²,即1²+x²=(3−x)²,解得x=$\frac{4}{3}$,所以BP=3−$\frac{4}{3}$=$\frac{5}{3}$(cm),所以CA+AB+BP=4+5+$\frac{5}{3}$=$\frac{32}{3}$(cm),此时t=$\frac{32}{3}$÷1=$\frac{32}{3}$.故t的值为$\frac{32}{3}$.
(2)如图2,当CP=CB时,△BCP为等腰三角形,若点P在CA上,则t=$\frac{3}{1}=3$;如图3,当BP=BC=3cm时,△BCP为等腰三角形,则AP=AB−BP=2cm,所以t=(4+2)÷1=6;如图4,若点P在AB上,CP=CB=3cm,过点C作CD⊥AB于点D,则根据直角三角形的面积法,得CD=$\frac{12}{5}$.在Rt△BCD中,由勾股定理,得BD=$\frac{9}{5}$,所以PB=2BD=$\frac{18}{5}$,所以CA+AP=4+5−$\frac{18}{5}=5.4$,此时t=5.4÷1=5.4;如图5,当PC=PB时,△BCP为等腰三角形,过点P作PD⊥BC于点D,则BD=CD,所以AP=BP=$\frac{1}{2}$AB=$\frac{5}{2}$,所以t=(4+$\frac{5}{2}$)÷1=6.5.综上所述,当t的值为3或5.4或6或6.5时,△BCP为等腰三角形.
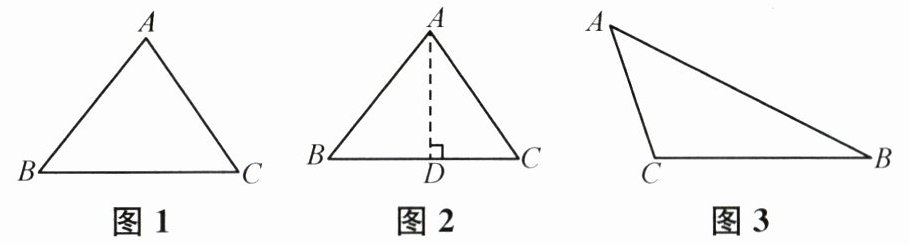
25. (10分)在$\triangle ABC$中,$BC = a$,$CA = b$,$AB = c$。若$\angle C$为直角,则$a^{2} + b^{2} = c^{2}$;若$\angle C$为锐角或钝角,则$a^{2} + b^{2}与c^{2}$之间有怎样的大小关系呢?我们一起进行探究吧。
(1)阅读并填空:如图1,若$\angle C$为锐角,则$a^{2} + b^{2}>c^{2}$。
证明:如图2,过点$A作AD\perp BC于点D$,则$BD = BC - CD = a - CD$。
在$Rt\triangle ABD$中,$AD^{2} = AB^{2} - BD^{2}$,
在$Rt\triangle ACD$中,$AD^{2} = $______,
所以______,
即$c^{2} - (a - CD)^{2} = b^{2} - CD^{2}$,
所以$a^{2} + b^{2} - c^{2} = 2a\cdot CD$。
因为$a>0$,$CD>0$,所以$a^{2} + b^{2} - c^{2}>0$,即$a^{2} + b^{2}>c^{2}$。
(2)解答问题:如图3,若$\angle C$为钝角,试推导$a^{2} + b^{2}与c^{2}$的大小关系。
(1)阅读并填空:如图1,若$\angle C$为锐角,则$a^{2} + b^{2}>c^{2}$。
证明:如图2,过点$A作AD\perp BC于点D$,则$BD = BC - CD = a - CD$。
在$Rt\triangle ABD$中,$AD^{2} = AB^{2} - BD^{2}$,
在$Rt\triangle ACD$中,$AD^{2} = $______,
所以______,
即$c^{2} - (a - CD)^{2} = b^{2} - CD^{2}$,
所以$a^{2} + b^{2} - c^{2} = 2a\cdot CD$。
因为$a>0$,$CD>0$,所以$a^{2} + b^{2} - c^{2}>0$,即$a^{2} + b^{2}>c^{2}$。
(2)解答问题:如图3,若$\angle C$为钝角,试推导$a^{2} + b^{2}与c^{2}$的大小关系。

答案:
(1)AC² - CD² AB² - BD²=AC² - CD²
(2)a² + b²<c².理由如下:如图,过点A作AD⊥BC交BC的延长线于点D,则BD=BC+CD=a+CD.在Rt△ABD中,AD²=AB²−BD²,在Rt△ACD中,AD²=AC²−CD²,所以AB²−BD²=AC²−CD²,即c²−(a+CD)²=b²−CD²,所以a² + b²−c²=−2a·CD.因为a>0,CD>0,所以a² + b²−c²<0,即a² + b²<c².
(1)AC² - CD² AB² - BD²=AC² - CD²
(2)a² + b²<c².理由如下:如图,过点A作AD⊥BC交BC的延长线于点D,则BD=BC+CD=a+CD.在Rt△ABD中,AD²=AB²−BD²,在Rt△ACD中,AD²=AC²−CD²,所以AB²−BD²=AC²−CD²,即c²−(a+CD)²=b²−CD²,所以a² + b²−c²=−2a·CD.因为a>0,CD>0,所以a² + b²−c²<0,即a² + b²<c².
查看更多完整答案,请扫码查看


