《2025年课时夺冠九年级数学上册湘教版》

19. （6分）解下列方程：
（1）$3x^2 - 5x - 2 = 0$；
（2）$3(x - 4)^2 = 16 - x^2$.

答案： 解：
(1)这里$ a = 3 $，$ b = -5 $，$ c = -2 $。因而$ b ^ { 2 } - 4 a c = ( - 5 ) ^ { 2 } - 4 \times 3 \times ( - 2 ) = 49 ＞ 0 $，所以$ x = \frac { - ( - 5 ) \pm \sqrt { 49 } } { 2 \times 3 } = \frac { 5 \pm 7 } { 6 } $。因此，原方程的根为$ x _ { 1 } = 2 $，$ x _ { 2 } = - \frac { 1 } { 3 } $。
(2)原方程可化为$ 3 ( x - 4 ) ^ { 2 } + ( x + 4 ) ( x - 4 ) = 0 $。把方程左边因式分解，得$ ( x - 4 ) [ 3 ( x - 4 ) + ( x + 4 ) ] = 0 $，由此得$ x - 4 = 0 $或$ 4 x - 8 = 0 $，解得$ x _ { 1 } = 4 $，$ x _ { 2 } = 2 $。

20. （6分）已知关于$x$的方程$x^2 + (2m - 1)x + 4 = 0$有两个相等的实数根，求$m$的值.

答案： 解：
∵关于$ x $的方程有两个相等的实数根，
∴$ \Delta = ( 2 m - 1 ) ^ { 2 } - 4 \times 1 \times 4 = 0 $，
∴$ ( 2 m - 1 ) ^ { 2 } = 16 $，
∴$ 2 m - 1 = \pm 4 $，解得$ m _ { 1 } = \frac { 5 } { 2 } $，$ m _ { 2 } = - \frac { 3 } { 2 } $。

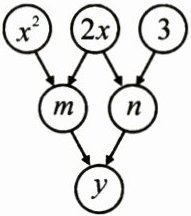
21. （8分）如图，约定上方相邻两数之和等于这两数下方箭头共同指向的数.
（1）当$m = 0$时，求$x$的值；
（2）当$y = 8$时，求$n$的值.

答案： 解：
(1)由题意，得当$ m = 0 $时，$ x ^ { 2 } + 2 x = 0 $，解得$ x _ { 1 } = 0 $，$ x _ { 2 } = - 2 $，
∴$ x $的值为0或-2。
(2)由题意，得$ m = x ^ { 2 } + 2 x $，$ n = 2 x + 3 $。
∵$ m + n = y = 8 $，
∴$ x ^ { 2 } + 2 x + 2 x + 3 = 8 $，解得$ x _ { 1 } = 1 $，$ x _ { 2 } = - 5 $。当$ x = 1 $时，$ n = 2 \times 1 + 3 = 5 $；当$ x = - 5 $时，$ n = 2 \times ( - 5 ) + 3 = - 7 $，
∴$ n $的值为5或-7。